Monthly Archives: February 2013

High-Frequency Financial Trading with Multivariate Direct Filtering Part Deux: Index Futures

Posted on by
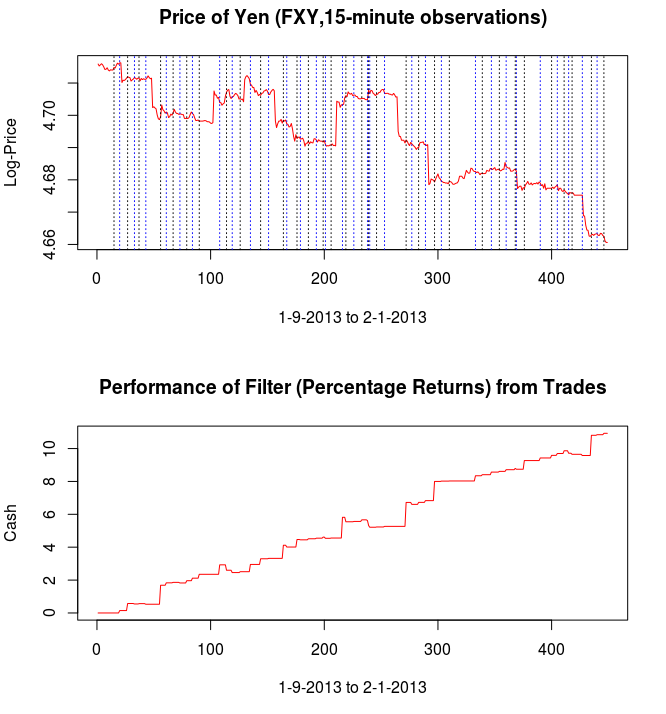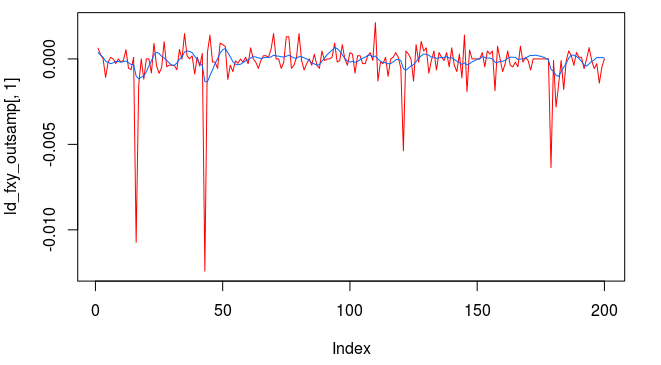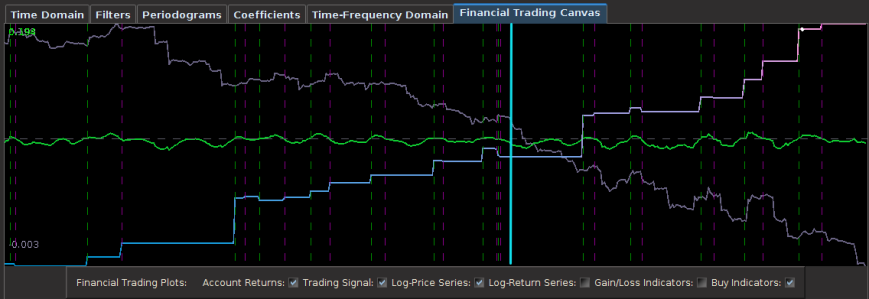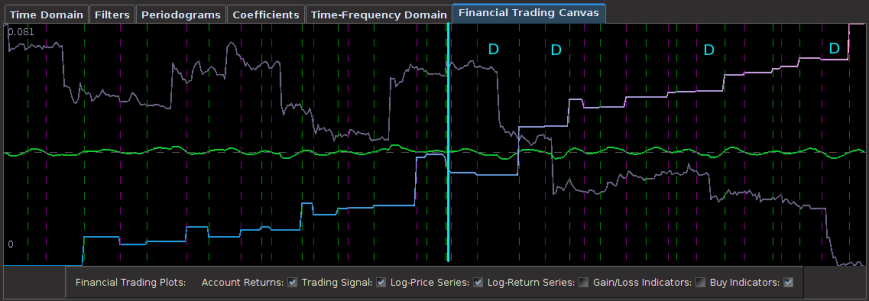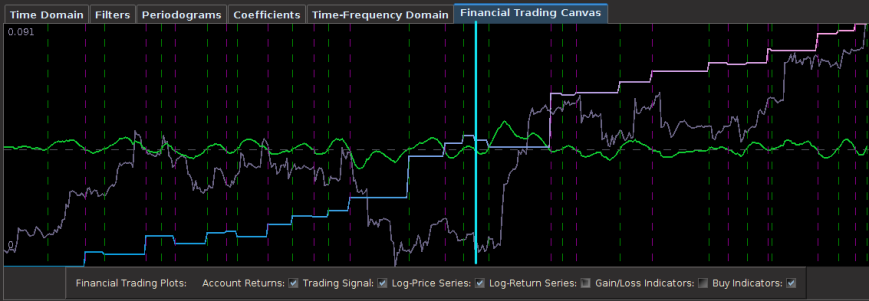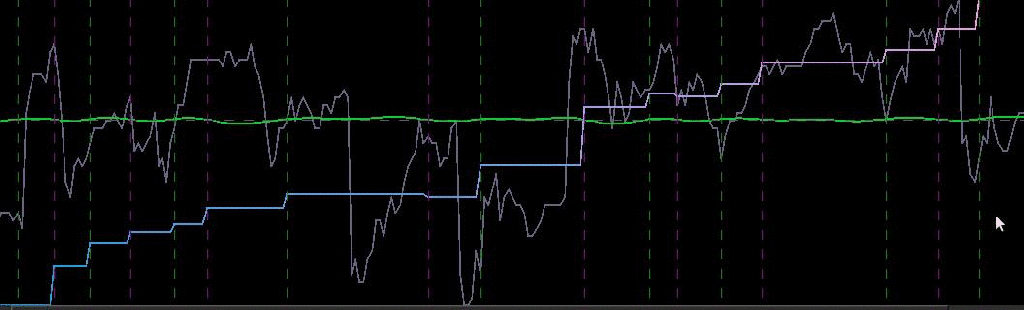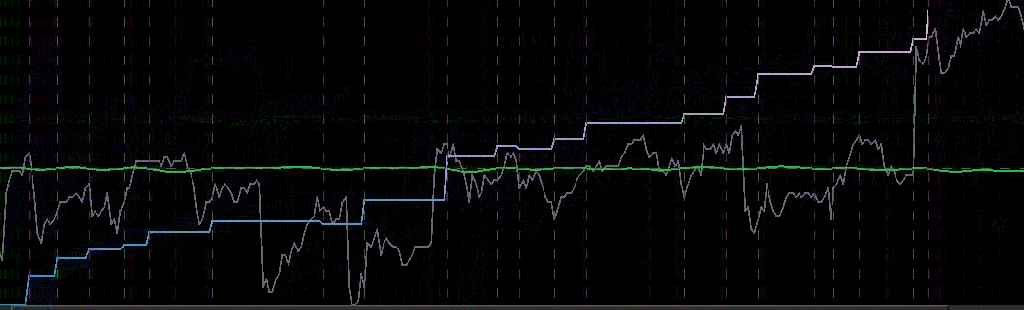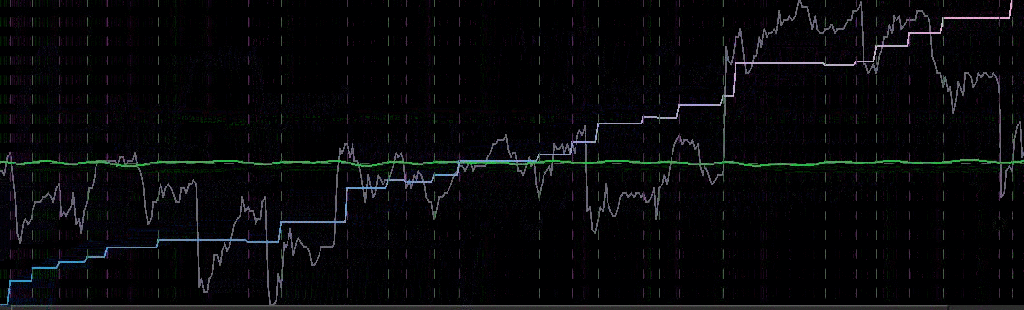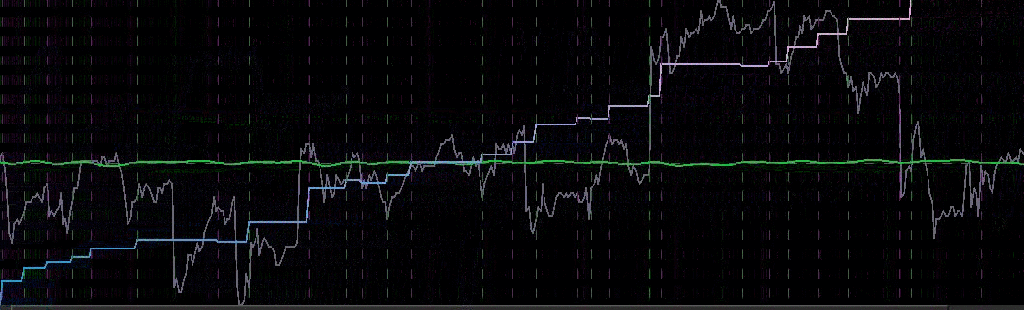
optimisedstxe

Out-of-sample performance (cash, blue-to-pink line) of an MDFA low-pass filter built using the approach discussed in this article on the STOXX Europe 50 index futures with expiration March 18th (STXEH3) for 200 15-minute interval log-return observations. Only one small loss out-of-sample was recorded from the period of Jan 18th through February 1st, 2013.

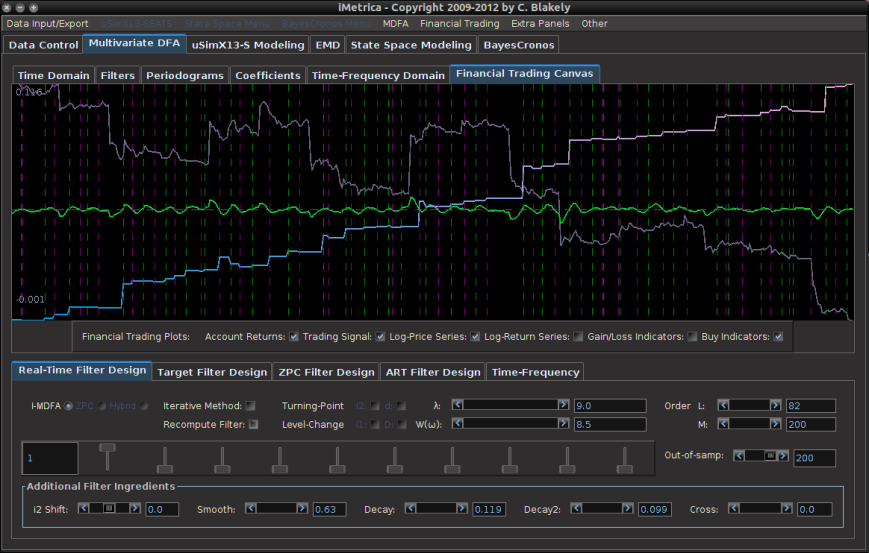
Continuing along the trend of my previous installment on strategies and performances of high-frequency trading using multivariate direct filtering, I take on building trading signals for high-frequency index futures, where I will focus on the STOXX Europe 50 Index, S&P 500, and the Australian Stock Exchange Index. As you will discover in this article, these filters that I build using MDFA in iMetrica have yielded some of the best performing trading signals that I have seen using any trading methodology.  My strategy as I’ve been developing throughout my previous articles on MDFA has not changed much, except for one detail that I will discuss throughout and will be a major theme of this article, and that relates to an interesting structure found in index futures series for intraday returns. The structure is related to the close-to-open variation in the price, namely when the price at close of market hours significantly differs from the price at open. an effect I’ve mentioned in my previous two articles dealing with high(er)-frequency (or intraday) log-return data. I will show how MDFA can take advantage of this variation in price and profit from each one by ‘predicting’ with the extracted signal the jump or drop in the price at the open of the next trading day.

The frequency of observations on the index that are to be considered for building trading filters using MDFA is typically only a question of taste and priorities.  The beauty of MDFA lies in not only the versatility and strength in building trading signals for virtually any financial trading priorities, but also in the independence on the underlying observation frequency of the data. In my previous articles, I’ve considered and built high-performing strategies for daily, hourly, and 15 minute log returns, where the focus of the strategy in building the signal began with viewing the periodogram as the main barometer in searching for optimal frequencies on which one should set the low-pass cutoff for the extracting target filter \Gamma function.

Index futures, as in a futures contract on a financial index, as we will see in this article present no new challenges. With the success I had on the 15-minute return observation frequency that I utilized in my previous article in building a signal for the Japanese Yen, I will continue to use the 15 minute intervals for the index futures where I hope to shed some more light on the filter selection process. This includes deducing properties of the intrinsically optimal spectral peaks to trade on. To do this, I present a simple approach I take in these examples by first setting up a bandpass filter over the spectral peak in the periodogram and then study the in-sample and out-of-sample characteristics of this signal, both in performance and consistency. So without further ado, I present my experiments with financial trading on index futures using MDFA, in iMetrica.

STOXX Europe 50 Index (STXE H3, Expiration March 18 2013)

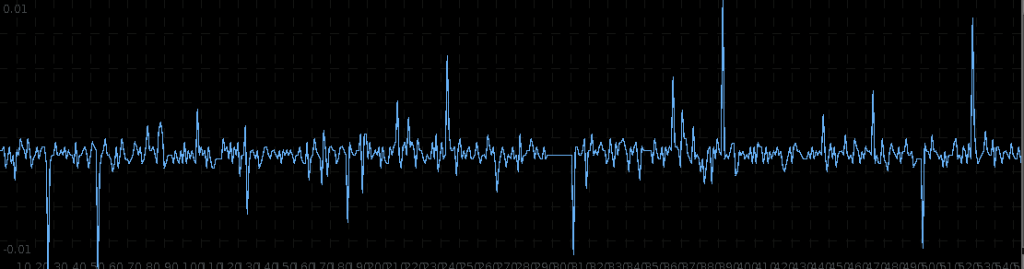
The STOXX Europe 50 Index, Europe’s leading Blue-chip index, provides a representation of sector leaders in Europe. The index covers 50 stocks from 18 European countries and has the highest trading volume of any European index. One of the first things to notice with the 15-minute log-returns of STXE are the frequent large spikes. These spikes will occur every 27 observations at 13:30 (UTC time zone) due to the fact that there are 26 15-minute periods during the trading hours. These spikes represent the close-to-open jumps that the STOXX Europe 50 index has been subjected to and then reflected in the price of the futures contract. With this ‘seasonal’ pattern so obviously present in the log-return data, the frequency effects of this pattern should be clearly visible in the periodogram of the data. The beauty of MDFA (and iMetrica) is that we have the ability to explicitly engineer a trading signal to take advantage of this ‘seasonal’ pattern by building an appropriate extractor \Gamma.

Figure 1: Log-returns of STXE for the 15-min observations from 1-4-2013 to 2-1-2013

Figure 1: Log-returns of STXE for the 15-min observations from 1-4-2013 to 2-1-2013

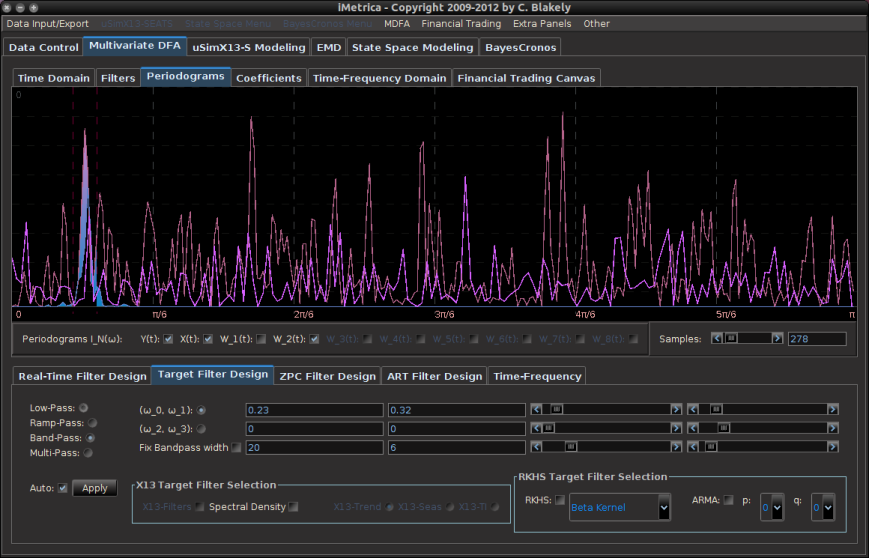
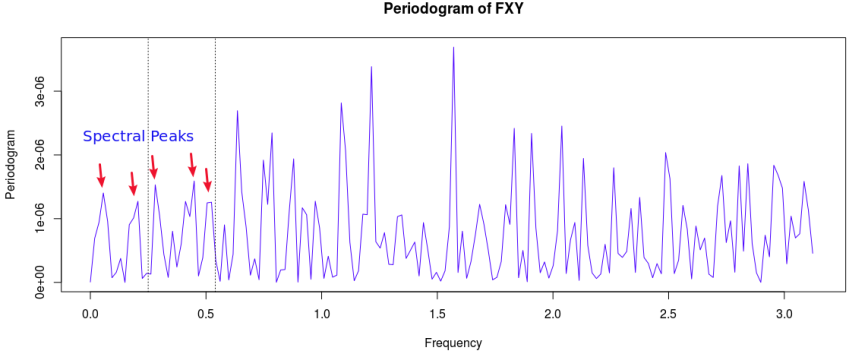
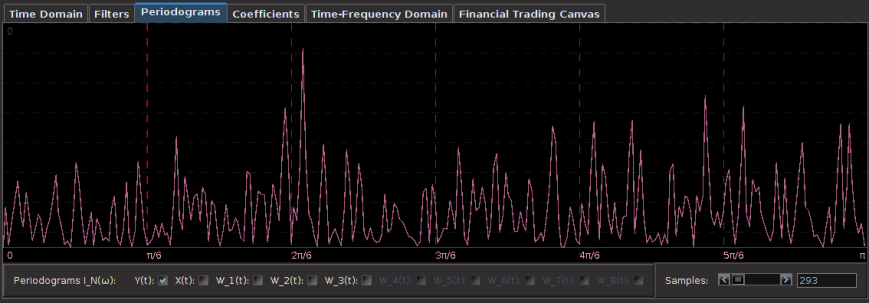
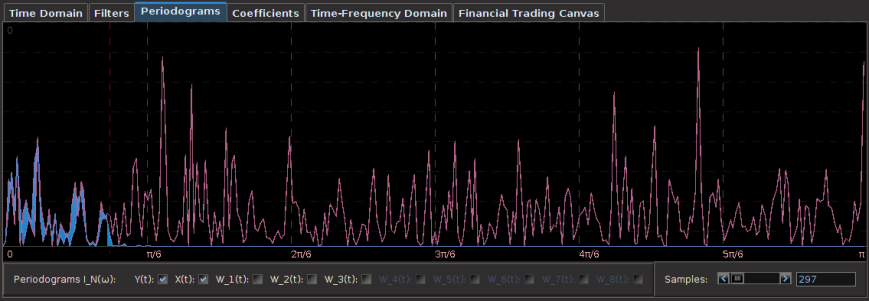
Regarding the periodogram of the data, Figure 2 depicts the periodograms for the 15 minute log-returns of STXE (red) and the explanatory series (pink) together on the same discretized frequency domain. Notice that in both log-return series, there is a principal spectral peak found between .23 and .32.   The trick is to localize the spectral peak that accounts for the cyclical pattern that is brought about by the close-to-open variation between 20:00 and 13:30 UTC.

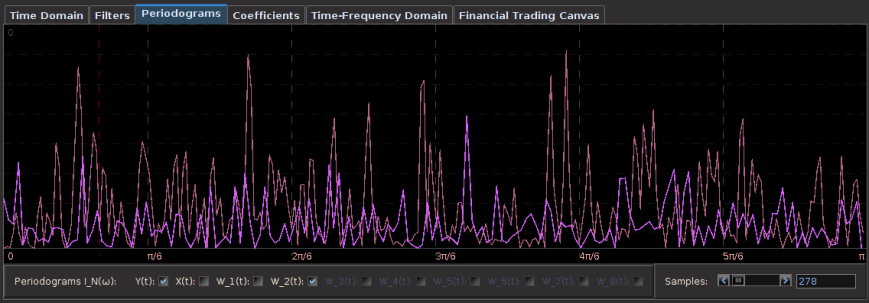
Figure 2: The periodograms for the 15 minute log-returns of STXE (red) and the explanatory series (pink).

Figure 2: The periodograms for the 15 minute log-returns of STXE (red) and the explanatory series (pink).

In order to see the effects of the MDFA filter when localizing this spectral peak, I use my target \Gamma builder interface in iMetrica to set the necessary cutoffs for the bandpass filter directly covering both spectral peaks of the log-returns, which are found between .23 and .32. This is shown in Figure 3, where the two dashed red lines show indicate the cutoffs and spectral peak is clearly inside these two cutoffs, with the spectral peak for both series occurring in the vicinity of \pi/12.  Once the bandpass target \Gamma was fixed on this small frequency range, I set the regularization parameters for the filter coefficients to be \lambda_{smooth} = .86,   \lambda_{decay} = .11,  and \lambda_{decay2} = .11.

Figure 3: Choosing the cutoffs for the band pass filter to localize the spectral peak.

Figure 3: Choosing the cutoffs for the band pass filter to localize the spectral peak.

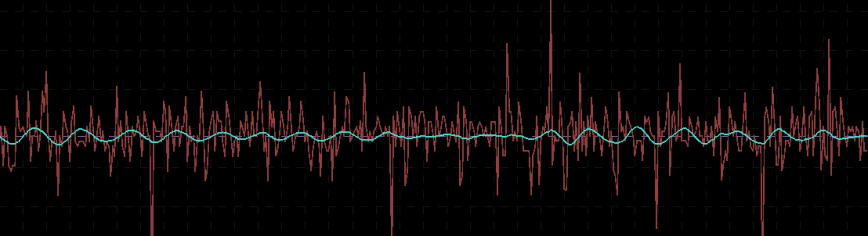
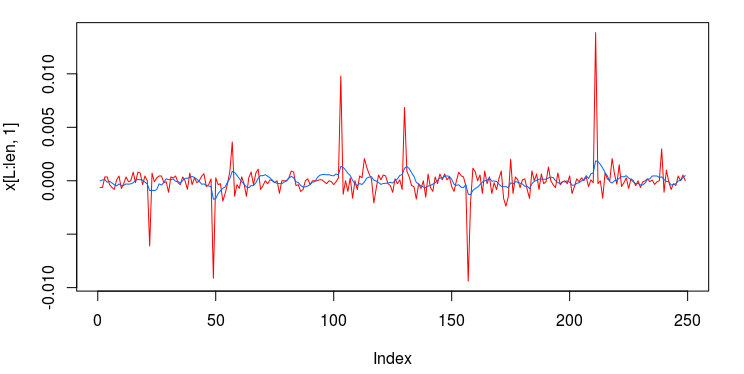
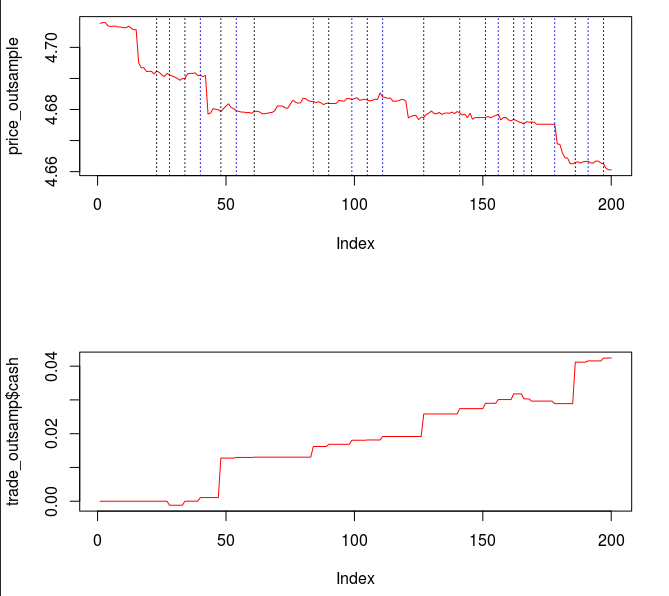
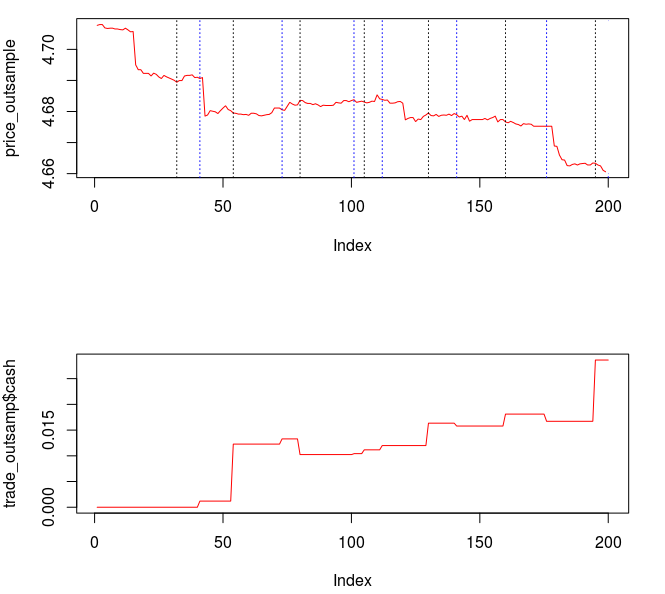
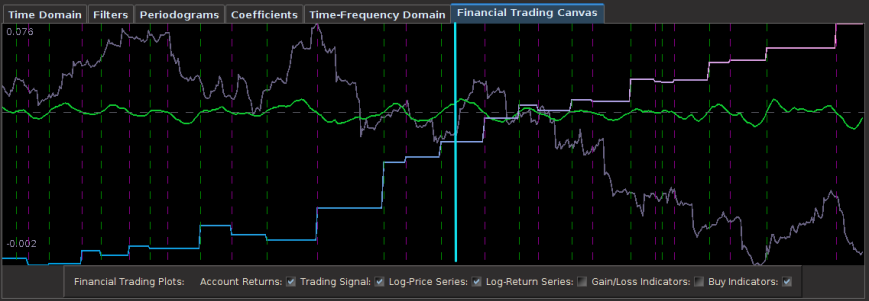
Pinpointing this frequency range that zooms in on the largest spectral peak generates a filter that acts on the intrinsic cycles found in the 15 minute log-returns of the STXE futures index. The resulting trading signal produced by this spectral peak extraction is shown in Figure 4, with the returns (blue to pink line) generated from the trading signal (green) , and the price of the STXE futures index in gray. The cyclical effects in the signal include the close-to-open variations in the data. Notice how the signal predicts the variation of the close-to-open price in the index quite well, seen from the large jumps or falls in price every 27 observations. The performance of this simple design in extracting the spectral peak of STXE yields a 4 percent ROI on 200 observations out-of-sample with only 3 losses out of 20 total trades (85 percent trade success rate), with two of them being accounted for towards the very end of the out-of-sample observations in an uncharacteristic volatile period occurring on January 31st 2013.

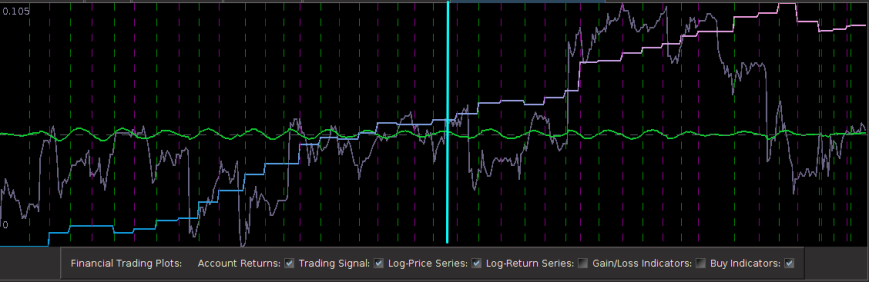
Figure : The performance in-sample and out-of-sample of the spectral peak localizing bandpass filter.

Figure 4: The performance in-sample and out-of-sample of the spectral peak localizing bandpass filter.

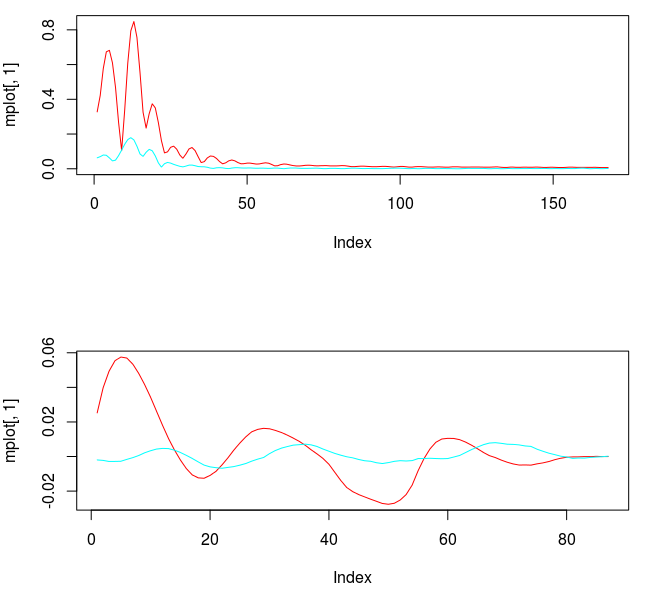
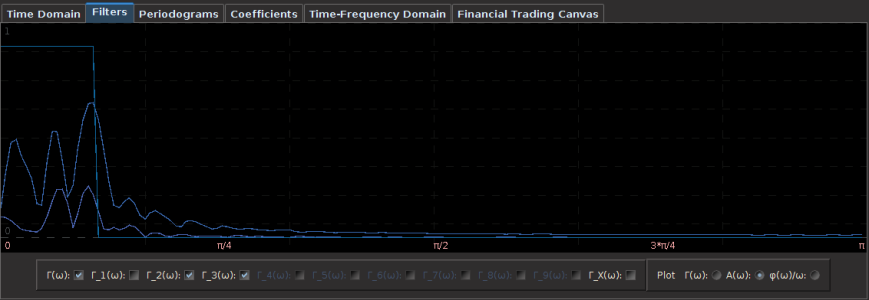
The two concurrent frequency response (transfer) functions for the two filters acting on the STXE log-return data (purple) and the explanatory series (blue), respectively, are plotted below in Figure 5. Notice the presence of the spectral peaks for both series being accounted for in the vicinity of the frequency \pi/12, with mild damping at the peak. Slow damping of the noise in the higher frequencies is aided by the addition of a smoothing expweight parameter that was set at \alpha = 4.

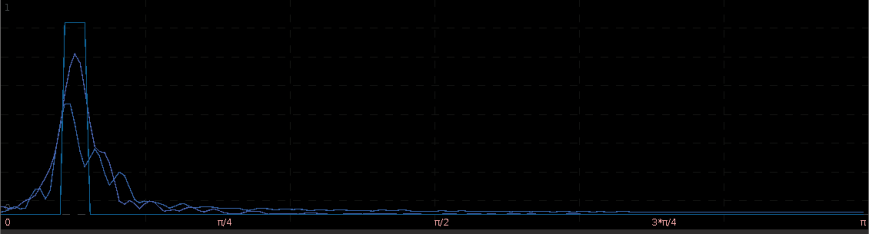
Figure : The performance in-sample and out-of-sample of the spectral peak localizing bandpass filter.

Figure 5: The concurrent frequency response functions of the localizing spectral peak band-pass filter.

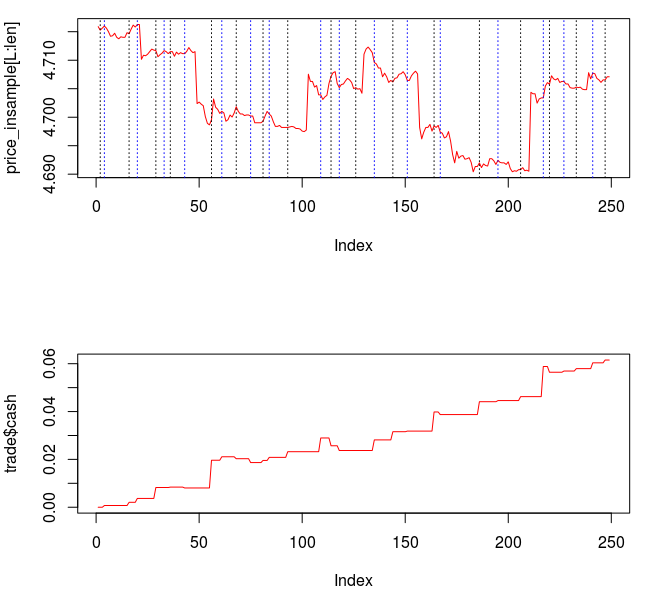
With the ideal characteristics of a trading signal quite present in this simple bandpass filter, namely smooth decaying filter coefficients, in-sample and out-of-sample performance properties identical, and accurate, consistent trading patterns, it would be hard to imagine on improving the trading signal for this European futures index even more. But we can. We simply keep the spectral peak frequencies intact, but also account for the local bias in log-return data by extending the lower cutoff to frequency zero. This will provide improved systematic trading characteristics by not only predicting the close-to-open variation and jumps, but also handling upswings and downswings, and highly volatile periods much better.

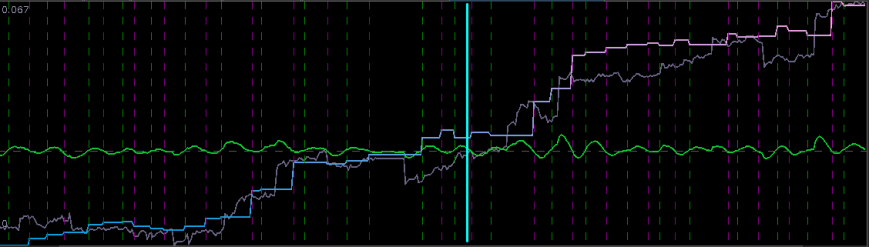
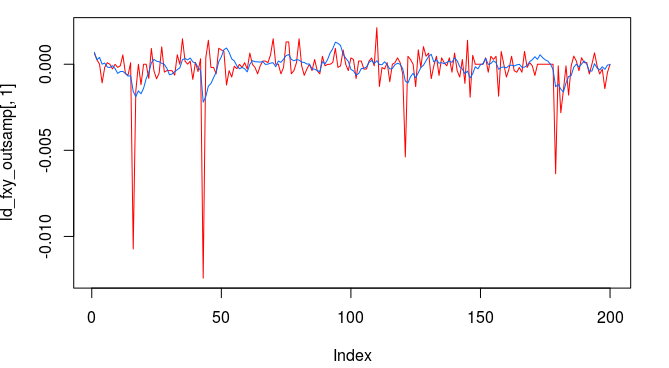
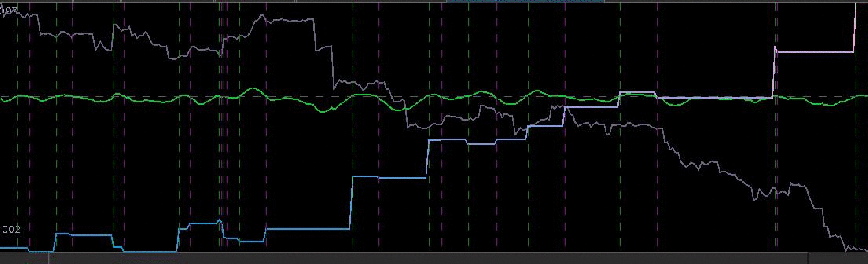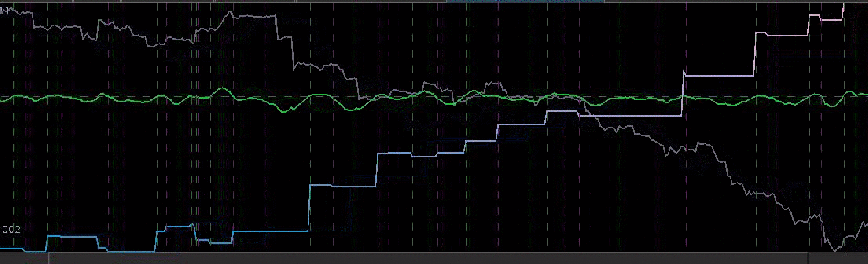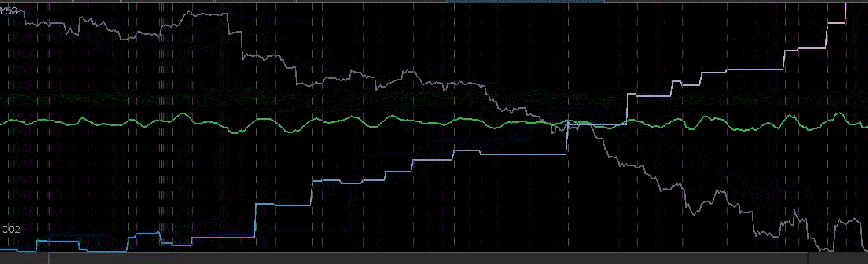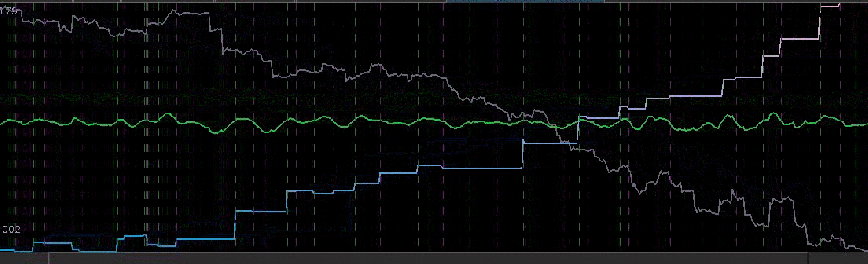
In this new design, I created a low-pass filter by keeping the upper cutoff \omega_1 from the band-pass design and setting the lower cutoff to 0. I also increased the smoothing parameter to $\alpha = 32$. In this newly designed filter, we see a vast improvement in the trading structure. As before, the filter was able to deduce the direction of every single close-to-open jump during the 200 out-of-sample observations, but notice that it was also able to become much more flexible in the trading during any upswing/downswing and volatile period. This is seen in more detail in Figure 7, where I added the letter ‘D’ to each of the 5 major buy/sell signals occurring before close.

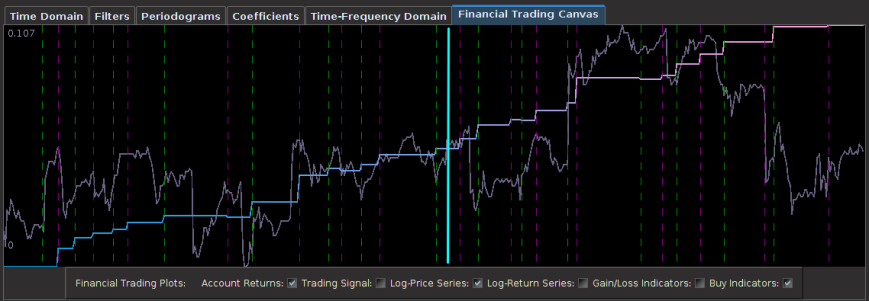
Figure : Performance of filter both in-sample (left of cyan line) and on 210 observations out-of-sample (right of cyan line).

Figure 6: Performance of filter both in-sample (left of cyan line) and on 210 observations out-of-sample (right of cyan line).

Notice that the signal predicted the jump correctly for each of these major jumps, resulting in large returns. For example, at the first “D” indicator,  the signal indicated sell/short (magenta dashed line) the STXE future index 5 observations before close, namely at 18:45 UTC, before market close at 20:00 UTC. Sure enough, the price of the STXE contract went down during overnight trading hours and opened far below the previous days close, with the filter signaling a buy (green dashed line) 45 minutes into trading. At the mark of the second “D”, we see that on the final observation before market close, the signal produced a buy/long indication, and indeed, the next day the price of the future jumped significantly.

Figure : Zooming in on the out-of-sample performance and showing all the signal responses that predicted the major close-to-open jumps.

Figure 7: Zooming in on the out-of-sample performance and showing all the signal responses that predicted the major close-to-open jumps.

Only two very small losses of less than .08 percent were accounted for.  One advantage of including the frequency zero along with the spectral peak frequency of STXE is that the local bias can help push-up or pull-down the signal resulting in a more ‘patient’ or ‘diligent’ filter that can better handle long upswings/downswings or volatile periods. This is seen in the improvement of the performance towards the end of the 200 observations out-of-sample, where the filter is more patient in signaling a sell/short after the previous buy. Compare this with the end of the performance from the band-pass filter, Figure 4.  With this trading signal out-of-sample, I computed a 5 percent ROI on the 200 observations out-of-sample with only 2 small losses. The trading statistics for the entire in-sample combined with out-of-sample are shown in Figure 8.

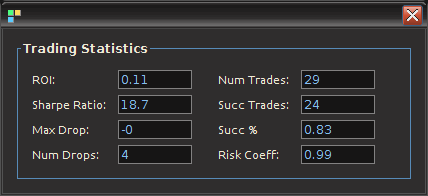
Figure 9: The total performance statistics of the STXEH3 trading signal in-sample plus out-of-sample.

Figure 8: The total performance statistics of the STXEH3 trading signal in-sample plus out-of-sample. The max drop indicates -0 due to the fact that there was a truncation to two decimal places. Thus the losses were less than .01.

S&P 500 Futures Index (ES H3, Expiration March 18 2013)

In this experiment trading S&P 500 future contracts (E-mini) on observations of 15 minute intervals from Jan 4th to Feb 1st 2013, I apply the same regimental approach as before.  In looking at the log-returns of ESH3 shown in Figure 10, the effect of close-to-open variation seem to be much less prominent here compared to that on the STXE future index. Because of this, the log-returns seem to be much closer to ‘white noise’ on this index. Let that not perturb our pursuit of a high performing trading signal however. The approach I take for extracting the trading signal, as always, begins with the periodogram.

The log-return data of ES H3 at 15 minute intervals from 1-4-2013 to 2-1-2013.

Figure 10: The log-return data of ES H3 at 15 minute intervals from 1-4-2013 to 2-1-2013.

As the large variations in the close-to-open price are not nearly as prominent, it would make sense that the same spectral peak found before at near \pi/12 is not nearly as prominent either. We can clearly see this in the periodogram plotted below in Figure 11. In fact, the spectral peak at \pi/12 is slightly larger in the explanatory series (pink), thus we should still be able to take advantage of any sort of close-to-open variation that exists in the E-min future index.

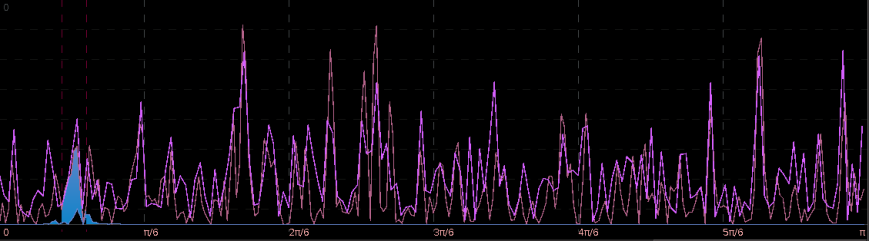
Figure 13: Periodograms of ES H3 log-returns (red) and the explanatory series (pink). The red dashed vertical lines are framing the spectral peak between .23 and .32.

Figure 11: Periodograms of ES H3 log-returns (red) and the explanatory series (pink). The red dashed vertical lines are framing the spectral peak between .23 and .32.

With this spectral peak extracted from the series, the resulting trading signal is shown in Figure 12 with the performance of the bandpass signal shown in Figure 13.

Figure 12: The signal built from the extracted spectral peak and the log-return ESH3 data.

Figure 12: The signal built from the extracted spectral peak and the log-return ESH3 data.

One can clearly see that the trading signal performs very well during the consistent cyclical behavior in the ESH3 price, However, when breakdown occurs in this stochastic structure and follows more prominently another frequency, the trading signal dies and no longer trades systematically taking advantage of the intrinsic cycle found near \pi/12. This can be seen in the middle 90 or so observations. The price can be seen to follow more closely a random walk and the trading becomes inconsistent. After this period of 90 or so observations however, just after the beginning of the out-of-sample period, the trajectory of the ESH3 follows back on its consistent course with a \pi/12 cyclical component it had before.

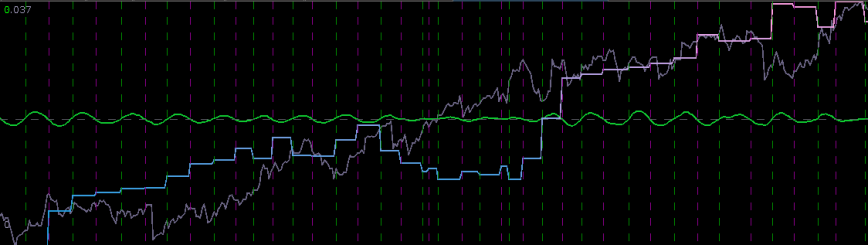
Figure 13: The performance in-sample and out-of-sample of the simple bandpass filter extracting the spectral peak.

Figure 13: The performance in-sample and out-of-sample of the simple bandpass filter extracting the spectral peak.

Now to improve on these results, we include the frequency zero by moving the lower cutoff of the previous band-pass filter to $\latex \omega_0 = 0$.  As I mentioned before, this lifts or pushes down the signal from the local bias and will trade much more systematically. I then lessened the amount of smoothing in the expweight function to \alpha = 24, down from \alpha = 36 as I had on the band-pass filter.  This allows for slightly higher frequencies than \pi/12 to be traded on. I then proceeded to adjust the regularization parameters to obtain a healthy dosage of smoothness and decay in the coefficients. The result of this new low-pass filter design is shown in Figure 14.

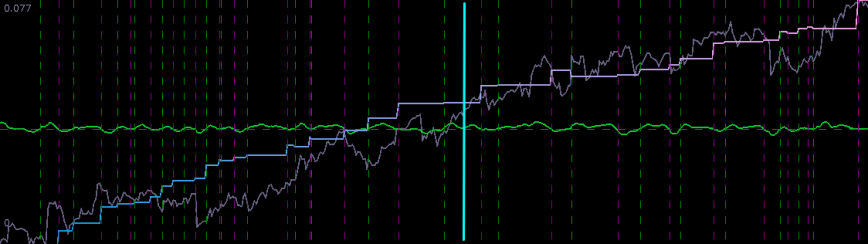
Figure 11: Performance out-of-sample (right of cyan line) of the ES H3 filter on 200 15 minute observations.

Figure 14: Performance out-of-sample (right of cyan line) of the ES H3 filter on 200 15 minute observations.

The improvement in the overall systematic trading and performance is clear. Most of the major improvements came from the middle 90 points where the trading became less cyclical. With 6 losses in the band-pass design during this period alone, I was able to turn those losses into two large gains and no losses.  Only one major loss was accounted for during the 200 observation out-of-sample testing of filter from January 18th to February 1st, with an ROI of nearly 4 percent during the 9 trading days. As with the STXE filter in the previous example, I was able to successfully build a filter that correctly predicts close-to-open variations, despite the added difficulty that such variations were much smaller. Both in-sample and out-of-sample, the filter performs consistently, which is exactly what one strives for thanks to regularization.

ASX Futures (YAPH3, Expiration March 18, 2013)

In the final experiment, I build a trading signal for the Australian Stock Exchange futures, during the same period of the previous two experiments. The log-returns show moderately large jumps/drops in price during the entire sample from Jan 4th to Feb 1st, but not quite as large as in the STXE index. We still should be able to take advantage of these close-to-open variations.

YAPH3

Figure 15: The log-returns of the YAPH3 in 15-minute interval observations.

In looking at the periodograms for both the YAPH3 15 minute log-returns (red) and the explanatory series (pink), it is clear that the spectral peaks don’t align like they did in the previous two exampls. In fact, there hardly exists a dominant spectral peak in the explanatory series, whereas the \pi/12 spectral peak in YAPH3 is very prominent. This ultimately might effect the performance of the filter, and consequently the trades. After building the low-pass filter and setting a high smoothing expweight parameter \alpha = 26.5, I then set the regularization parameters to be  \lambda_{smooth} = .85,   \lambda_{decay} = .11,  and \lambda_{decay2} = .11 (same as first example).

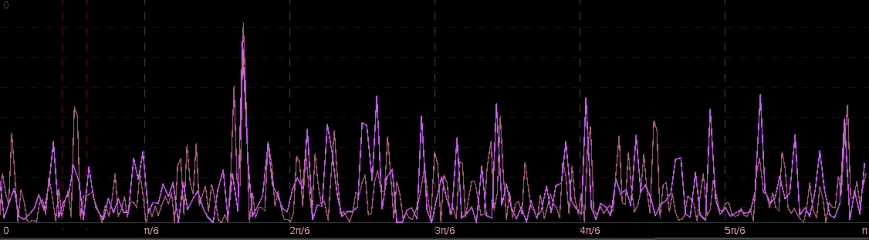
Figure : The periodograms for YAPH3 and explanatory series with spectral peak in YAPH3 framed by the red dashed lines.

Figure 16: The periodograms for YAPH3 and explanatory series with spectral peak in YAPH3 framed by the red dashed lines.

The performance of the filter in-sample and out-of-sample is shown in Figure 18. This was one of the more challenging index futures series to work with as I struggled finding an appropriate explanatory series (likely because I was lazy since it was late at night and I was getting tired). Nonetheless, the filter still seems to predict the close-to-open variation on the Australian stock exchange index fairly well. All the major jumps in price are accounted for if you look closely at the trades (green dashed lines are buys/long and magenta lines are sells/shorts) and the corresponding action on the price of the futures contract.   Five losses out-of-sample for a trade success ratio of 72 percent and an ROI out-of-sample on 200 observations of 4.2 percent.  As with all other experiments in building trading signals with MDFA, we check the consistency of the in-sample and out-of-sample performance, and these seem to match up nicely.

Figure : The out-of-sample performance of the low-pass filter on YAPH3.

Figure 18 : The out-of-sample performance of the low-pass filter on YAPH3.

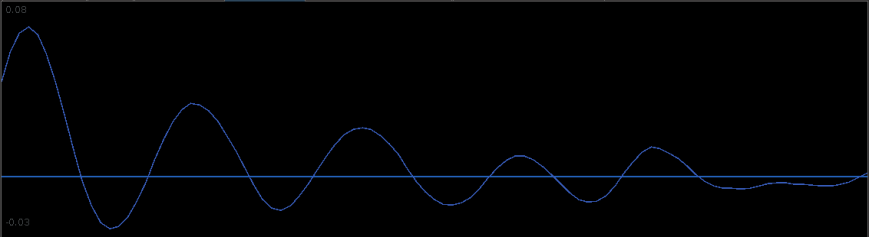
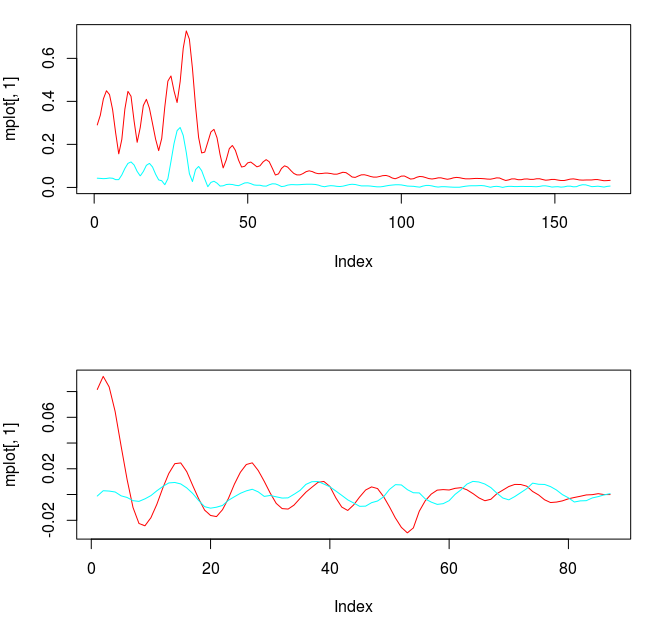
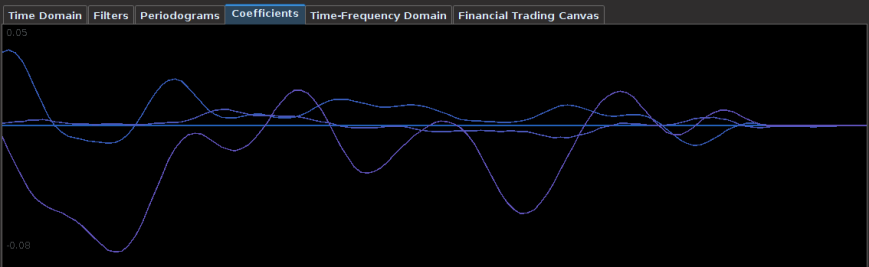
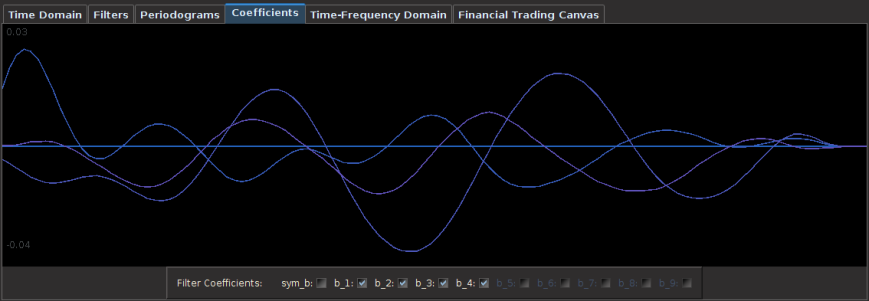
The filter coefficients for the YAPH3 log-difference series is shown in Figure 19. Notice the perfectly smooth undulating yet decaying structure of the coefficients as the lag increases. What a beauty.

Figure 16: Filter coefficients for the YAPH3 series.

Figure 19: Filter coefficients for the YAPH3 series.

Conclusion

Studying the trading performance of spectral peaks by first constructing band-pass filters to extract the signal corresponding to the peak in these index futures enabled me to understand how I can better construct the lowpass filter to yield even better performance. In these examples, I demonstrated that the close-to-open variation in the index futures price can be seen in the periodogram and thus be controlled for in the MDFA trading signal construction. This trading frequency corresponds to roughly \pi/12 in the 15 minute observation data that I had from Jan 4th to Feb 1st. As I witnessed in my empirical studies using iMetrica, this peak is more prominent when the close-to-open variations are larger and more often, promoting a very cyclical structure in the log-return data.  As I look deeper and deeper into studying the effects of extracting spectral peaks in the periodogram of financial data log-returns and the trading performance, I seem to improve on results even more and building the trading signals becomes even easier.

Stay tuned very soon for a tutorial using R (and MDFA) for one of these examples on high-frequency trading on index futures.  If you have any questions or would like to request a certain index future (out of one of the above examples or another) to be dissected in my second and upcoming R tutorial, feel free to shoot me an email.

Happy extracting!

High-Frequency Financial Trading on FOREX with MDFA and R: An Example with the Japanese Yen

Posted on by
In-sample (observations 1-235) and out-of-sample (observations 236-455) performance of the trading signal built in this tutorial using MDFA. (Top) The log price of the Yen (FXY) in 15 minute intervals and the trades generated by the trading signal. Here black line is a buy (long), blue is sell (short position). (Bottom) The returns accumulated (cash) generated by the trading, in percentage gained or lossed.

Figure 1: In-sample (observations 1-250) and out-of-sample performance of the trading signal built in this tutorial using MDFA. (Top) The log price of the Yen (FXY) in 15 minute intervals and the trades generated by the trading signal. Here black line is a buy (long), blue is sell (short position). (Bottom) The returns accumulated (cash) generated by the trading, in percentage gained or lost.

In my previous article on high-frequency trading in iMetrica on the FOREX/GLOBEX, I introduced some robust signal extraction strategies in iMetrica using the multidimensional direct filter approach (MDFA) to generate high-performance signals for trading on the foreign exchange and Futures market. In this article I take a brief leave-of-absence from my world of developing financial trading signals in iMetrica and migrate into an uber-popular language used in finance due to its exuberant array of packages, quick data management and graphics handling, and of course the fact that it’s free (as in speech and beer) on nearly any computing platform in the world.

This article gives an intro tutorial on using R for high-frequency trading on the FOREX market using the R package for MDFA (offered by Herr Doktor Marc Wildi von Bern) and some strategies that I’ve developed for generating financially robust trading signals. For this tutorial, I consider the second example given in my previous article where I engineered a trading signal for 15-minute log-returns of the Japanese Yen (from opening bell to market close EST).  This presented slightly new challenges than before as the close-to-open jump variations are much larger than those generated by hourly or daily returns. But as I demonstrated, these larger variations on close-to-open price posed no problems for the MDFA. In fact, it exploited these jumps and made large profits by predicting the direction of the jump. Figure 1 at the top of this article shows the in-sample (observations 1-250) and out-of-sample (observations 251 onward) performance of the filter I will be building in the first part of this tutorial. 

Throughout this tutorial, I attempt to replicate these results that I built in iMetrica and expand on them a bit using the R language and the implementation of the MDFA available in here.  The data that we consider are 15-minute log-returns of the Yen from January 4th to January 17th and I have them saved as an .RData file given by ld_fxy_insamp. I have an additional explanatory series embedded in the .RData file that I’m using to predict the price of the Yen. Additionally, I also will be using price_fxy_insamp which is the log price of Yen, used to compute the performance (buy/sells) of the trading signal. The ld_fxy_insamp will be used as the in-sample data to construct the filter and trading signal for FXY. To obtain this data so you can perform these examples at home, email me and I’ll send you all the necessary .RData files (the in-sample and out-of-sample data) in a .zip file. Taking a quick glance at the ld_fxy_insamp data, we see log-returns of the Yen at every 15 minutes starting at market open (time zone UTC). The target data (Yen) is in the first column along with the two explanatory series (Yen and another asset co-integrated with movement of Yen).

> head(ld_fxy_insamp)
[,1]           [,2]          [,3]
2013-01-04 13:30:00  0.000000e+00   0.000000e+00  0.0000000000
2013-01-04 13:45:00  4.763412e-03   4.763412e-03  0.0033465833
2013-01-04 14:00:00 -8.966599e-05  -8.966599e-05  0.0040635638
2013-01-04 14:15:00  2.597055e-03   2.597055e-03 -0.0008322064
2013-01-04 14:30:00 -7.157556e-04  -7.157556e-04  0.0020792190
2013-01-04 14:45:00 -4.476075e-04  -4.476075e-04 -0.0014685198

Moving on, to begin constructing the first trading signal for the Yen, we begin by uploading the data into our R environment, define some initial parameters for the MDFA function call, and then compute the DFTs and periodogram for the Yen.

load(paste(path.pgm,"ld_fxy_in15min.RData",sep=""))    #load in-sample log-returns of Yen
load(paste(path.pgm,"price_fxy_in15min.RData",sep="")) #load in-sample log-price of Yen

in_samp_lenprice_insample<-price_fxy_insamp

#setup some MDFA variables
x<-ld_fxy_insamp
len<-length(x[,1])
shift_constraint<-rep(0,length(x[1,])-1)
weight_constraint<-rep(0,length(x[1,])-1)
d<-0
plots<-T
lin_expweight<-F

# Compute DFTs and periodogram for initial analysis
spec_obj<-spec_comp(len,x,d)
weight_func<-spec_obj$weight_func
K<-length(weight_func[,1])-1
fxy_periodogram<-abs(spec_obj$weight_func[,1])^2

As I’ve mentioned in my previous articles, my step-by-step strategy for building trading signals always begin by a quick analysis of the periodogram of the asset being traded on. Holding the key to providing insight into the characteristics of how the asset trades, the periodogram is an essential tool for navigating how the extractor \Gamma is chosen. Here, I look for principal spectral peaks that correspond in the time domain to how and where my signal will trigger buy/sell trades. Figure 2 shows the periodogram of the 15-minute log-returns of the Japanese Yen during the in-sample period from January 4 to January 17 2013. The arrows point to the main spectral peaks that I look for and provides a guide to how I will define my \Gamma function. The black dotted lines indicate the two frequency cutoffs that I will consider in this example, the first being \pi/12 and the second at \pi/6. Notice that both cutoffs are set directly after a spectral peak, something that I highly recommend.  In high-frequency trading on the FOREX using MDFA, as we’ll see, the trick is to seek out the spectral peak which accounts for the close-to-open variation in the price of the foreign currency. We want to take advantage of this spectral peak as this is where the big gains in foreign currency trading using MDFA will occur.

Figure 2: Periodogram of FXY (Japanese Yen) along with spectral peaks and two different frequency cutoffs.

Figure 2: Periodogram of FXY (Japanese Yen) along with spectral peaks and two different frequency cutoffs.

In our first example we consider the larger frequency as the cutoff for \Gamma by setting it to \pi/6 (the right most line in the figure of the periodogram). I then initially set the timeliness and smoothness parameters, lambda and expweight to 0 along with setting all the regularization parameters to 0 as well. This will give me a barometer for where and how much to adjust the filter parameters. In selecting the filter length L, my empirical studies over numerous experiments in building trading signals using iMetrica have demonstrated that a ‘good’ choice is anywhere between 1/4 and 1/5 of the total in-sample length of the time series data.  Of course, the length depends on the frequency of the data observations (i.e. 15 minute, hourly, daily, etc.), but in general you will most likely never need more than L being greater than 1/4 the in-sample size. Otherwise, regularization can become too cumbersome to handle effectively. In this example, the total in-sample length is 335 and thus I set L= 82 which I’ll stick to for the remainder of this tutorial. In any case, the length of the filter is not the most crucial parameter to consider in building good trading signals. For a good robust selection of the filter parameters couple with appropriate explanatory series, the results of the trading signal with L= 80 compared with, say, L= 85 should hardly differ. If they do, then the parameterization is not robust enough.

After uploading both the in-sample log-return data along with the corresponding log price of the Yen for computing the trading performance, we the proceed in R to setting initial filter settings for the MDFA routine and then compute the filter using the IMDFA_comp function. This returns both the i_mdfa& object holding coefficients, frequency response functions, and statistics of filter, along with the signal produced for each explanatory series. We combine these signals to get the final trading signal in-sample. All this is all done in R as follows:


cutoff<-pi/6 #set frequency cutoff
Gamma<-((0:K)<(cutoff*K/pi)) #define Gamma

grand_mean<-F
Lag<-0
L<-82
lambda_smooth<-0
lambda_cross<-0
lambda_decay<-c(0.,0.) #regularization - decay

lambda<-0
expweight<-0
i1<-F
i2<-F
# compute the filter for the given parameter definitions
i_mdfa_obj<-IMDFA_comp(Lag,K,L,lambda,weight_func,Gamma,expweight,cutoff,i1,i2,weight_constraint,
lambda_cross,lambda_decay,lambda_smooth,x,plots,lin_expweight,shift_constraint,grand_mean)

# after computing filter, we save coefficients
bn<-i_mdfa_obj$i_mdfa$b

# now we build trading signal
trading_signal<-i_mdfa_obj$xff[,1] + i_mdfa_obj$xff[,2]

The resulting frequency response functions of the filter and the coefficients are plotted in the figure below.

Figure 3: The Frequency response functions of the filter and the filter coefficients

Figure 3: The Frequency response functions of the filter (top) and the filter coefficients (below)

Notice the abundance of noise still present passed the cutoff frequency. This is mollified by increasing the expweight smoothness parameter. The coefficients for each explanatory series show some correlation in their movement as the lags increase. However, the smoothness and decay of the coefficients leaves much to be desired. We will remedy this by introducing regularization parameters. Plots of the in-sample trading signal and the performance in-sample of the signal are shown in the two figures below. Notice that the trading signal behaves quite nicely in-sample. However, looks can be deceiving. This stellar performance is due in large part to a filtering phenomenon called overfitting. One can deduce that overfitting is the culprit here by simply looking at the nonsmoothness of the coefficients along with the number of freezed degrees of freedom, which in this example is roughly 174 (out of 174), way too high. We would like to get this number at around half the total amount of degrees of freedom (number of explanatory series x L).

Figure 4: The trading signal and the log-return data of the Yen.

Figure 4: The trading signal and the log-return data of the Yen.

The in-sample performance of this filter demonstrates the type of results we would like to see after regularization is applied.  But now comes for the sobering effects of overfitting. We apply these filter coeffcients to 200 15-minute observations of the Yen and the explanatory series from January 18 to February 1 2013 and compare with the characteristics in-sample. To do this in R, we first load the out-of-sample data into the R environment, and then apply the filter to the out-of-sample data that I defined as x_out.

load(paste(path.pgm,"ld_fxy_out15min.RData",sep=""))
load(paste(path.pgm,"price_fxy_out15min.RData",sep=""))
x_out<-rbind(ld_fxy_insamp,ld_fxy_outsamp) #bind the in-sample with out-of-sample data
xff<-matrix(nrow=out_samp_len,ncol=2)

#apply filter built in-sample
for(i in 1:out_samp_len)
{
  xff[i,]<-0
  for(j in 2:3)
  {
      xff[i,j-1]<-xff[i,j-1]+bn[,j-1]%*%x_out[335+i:(i-L+1),j]
  }
}
trading_signal_outsamp<-xff[,1] + xff[,2]     #assemble the trading signal out-of-sample
trade_outsamp<-trading_logdiff(trading_signal_outsamp,price_outsample,.0005)  #compute the performance

The plot in Figure 5 shows the out-of-sample trading signal. Notice that the signal is not nearly as smooth as it was in-sample. Overshooting of the data in some areas is also obviously present. Although the out-of-sample overfitting characteristics of the signal are not horribly suspicious, I would not trust this filter to produce stellar returns in the long run.

Figure : Filter applied to 200 15 minute observations of Yen out-of-sample to produce trading signal (shown in blue)

Figure 5 : Filter applied to 200 15 minute observations of Yen out-of-sample to produce trading signal (shown in blue)

Following the previous analysis of the mean-squared solution (no customization or regularization), we now proceed to clean up the problem of overfitting that was apparent in the coefficients along with mollifying the noise in the stopband (frequencies after \pi/6).  In order to choose the parameters for smoothing and regularization, one approach is to first apply the smoothness parameter first, as this will generally smooth the coefficients while acting as a ‘pre’-regularizer, and then advance to selecting appropriate regularization controls. In looking at the coefficients (Figure 3), we can see that a fair amount of smoothing is necessary, with only a slight touch of decay. To select these two parameters in R, one option is to use the Troikaner optimizer (found here) to find a suitable combination (I have a secret sauce algorithmic approach I developed for iMetrica for choosing optimal combinations of parameters given an extractor \Gamma and a performance indicator, although it’s lengthy (even in GNU C) and cumbersome to use, so I typically prefer the strategy discussed in this tutorial).   In this example, I began by setting the lambda_smooth to .5 and the decay to (.1,.1) along with an expweight smoothness parameter set to 8.5. After viewing the coefficients, it still wasn’t enough smoothness, so I proceeded to add more finally reaching .63, which did the trick. I then chose lambda to balance the effects of the smoothing expweight (lambda is always the last resort tweaking parameter).

lambda_smooth<-0.63
lambda_cross<-0.
lambda_decay<-c(0.119,0.099)
lambda<-9
expweight<-8.5

i_mdfa_obj<-IMDFA_comp(Lag,K,L,lambda,weight_func,Gamma,expweight,cutoff,i1,i2,weight_constraint,
lambda_cross,lambda_decay,lambda_smooth,x,plots,lin_expweight,shift_constraint,grand_mean)

bn<-i_mdfa_obj$i_mdfa$b    #save the filter coefficients

trading_signal<-i_mdfa_obj$xff[,1] + i_mdfa_obj$xff[,2]  #compute the trading signal
trade<-trading_logdiff(trading_signal[L:len],price_insample[L:len],0) #compute the in-sample performance

Figure 6 shows the resulting frequency response function for both explanatory series (Yen in red). Notice that the largest spectral peak found directly before the frequency cutoff at \pi/6 is being emphasized and slightly mollified (value near .8 instead of 1.0). The other spectral peaks below \pi/6 are also present. For the coefficients, just enough smoothing and decay was applied to keep the lag, cyclical, and correlated structure of the coefficients intact, but now they look much nicer in their smoothed form. The number of freezed degrees of freedom has been reduced to approximately 102.

Figure : The frequency response functions and the coefficients after regularization and smoothing have been applied.

Figure 6: The frequency response functions and the coefficients after regularization and smoothing have been applied (top). The smoothed coefficients with slight decay at the end (bottom). Number of freezed degrees of freedom is approximately 102 (out of 172).

Along with an improved freezed degrees of freedom and no apparent havoc of overfitting, we apply this filter out-of-sample to the 200 out-of-sample observations in order to verify the improvement in the structure of the filter coefficients (shown below in Figure 7).  Notice the tremendous improvement in the properties of the trading signal (compared with Figure 5). The overshooting of the data has be eliminated and the overall smoothness of the signal has significantly improved. This is due to the fact that we’ve eradicated the presence of overfitting.

Figure : Out-of-sample trading signal with regularization.

Figure 7: Out-of-sample trading signal with regularization.

With all indications of a filter endowed with exactly the characteristics we need for robustness, we now apply the trading signal both in-sample and out of sample to activate the buy/sell trades and see the performance of the trading account in cash value. When the signal crosses below zero, we sell (enter short position) and when the signal rises above zero, we buy (enter long position).

The top plot of Figure 8 is the log price of the Yen for the 15 minute intervals and the dotted lines represent exactly where the trading signal generated trades (crossing zero). The black dotted lines represent a buy (long position) and the blue lines indicate a sell (and short position).  Notice that the signal predicted all the close-to-open jumps for the Yen (in part thanks to the explanatory series). This is exactly what we will be striving for when we add regularization and customization to the filter. The cash account of the trades over the in-sample period is shown below, where transaction costs were set at .05 percent. In-sample, the signal earned roughly 6 percent in 9 trading days and a 76 percent trading success ratio.

Figure : In-sample performance of the new filter and the trades that are generated.

Figure 8: In-sample performance of the new filter and the trades that are generated.

Now for the ultimate test to see how well the filter performs in producing a winning trading signal, we applied the filter to the 200 15-minute out-of-sample observation of the Yen and the explanatory series from Jan 18th to February 1st and make trades based on the zero crossing. The results are shown below in Figure 9. The black lines represent the buys and blue lines the sells (shorts). Notice the filter is still able to predict the close-to-open jumps even out-of-sample thanks to the regularization. The filter succumbs to only three tiny losses at less than .08 percent each between observations 160 and 180 and one small loss at the beginning, with an out-of-sample trade success ratio hitting 82 percent and an ROI of just over 4 percent over the 9 day interval.

Figure : Out-of-sample performance of the regularized filter on 200 out-of-sample 15 minute returns of the Yen.

Figure 9: Out-of-sample performance of the regularized filter on 200 out-of-sample 15 minute returns of the Yen. The filter achieved 4 percent ROI over the 200 observations and an 82 percent trade success ratio.

Compare this with the results achieved in iMetrica using the same MDFA parameter settings. In Figure 10, both the in-sample and out-of-sample performance are shown. The performance is nearly identical.

Figure : In-sample and out-of-sample performance of the Yen filter in iMetrica. Nearly identical with performance obtained in R.

Figure 10: In-sample and out-of-sample performance of the Yen filter in iMetrica. Nearly identical with performance obtained in R.

Example 2

Now we take a stab at producing another trading filter for the Yen, only this time we wish to identify only the lowest frequencies to generate a trading signal that trades less often, only seeking the largest cycles. As with the performance of the previous filter, we still wish to target the frequencies that might be responsible to the large close-to-open variations in the price of Yen. To do this, we select our cutoff to be \pi/12 which will effectively keep the largest three spectral peaks intact in the low-pass band of \Gamma.

For this new filter, we keep things simple by continuing to use the same regularization parameters chosen in the previous filter as they seemed to produce good results out-of-sample. The \lambda and expweight customization parameters however need to be adjusted to account for the new noise suppression requirements in the stopband and the phase properties in the smaller passband. Thus I increase the smoothing parameter and decreased the timeliness parameter (which only affects the passband) to account for this change. The new frequency response functions and filter coefficients for this smaller lowpass design are shown below in Figure 11. Notice that the second spectral peak is accounted for and only slightly mollified under the new changes. The coefficients still have the noticeable smoothness and decay at the largest lags.

Figure : Frequency response functions of the two filters and their corresponding coefficients.

Figure 11: Frequency response functions of the two filters and their corresponding coefficients.

To test the effectiveness of this new lower trading frequency design, we apply the filter coefficients to the 200 out-of-sample observations of the 15-minute Yen log-returns. The performance is shown below in Figure 12. In this filter, we clearly see that the filter still succeeds in predicting correctly the large close-to-open jumps in the price of the Yen. Only three total losses are observed during the 9 day period. The overall performance is not as appealing as the previous filter design as less amount of trades are made, with a near 2 percent ROI and 76 percent trade success ratio. However, this design could fit the priorities for a trader much more sensitive to transaction costs.

Figure : Out-of-sample performance of filter with lower cutoff.

Figure 12: Out-of-sample performance of filter with lower cutoff.

Conclusion

Verification and cross-validation is important, just as the most interesting man in the world knows.

Verification and cross-validation is important, just as the most interesting man in the world will tell you.

The point of this tutorial was to show some of the main concepts and strategies that I undergo when approaching the problem of building a robust and highly efficient trading signal for any given asset at any frequency. I also wanted to see if I could achieve similar results with the R MDFA package as my iMetrica software package. The results ended up being nearly parallel except for some minor differences. The main points I was attempting to highlight were in first analyzing the periodogram to seek out the important spectral peaks (such as ones associate with close-to-open variations) and to demonstrate how the choice of the cutoff affects the systematic trading.  Here’s a quick recap on good strategies and hacks to keep in mind.

Summary of strategies for building trading signal using MDFA in R:

  • As I mentioned before, the periodogram is your best friend. Apply the cutoff directly after any range of spectral peaks that you want to consider. These peaks are what generate the trades.
  • Utilize a choice of filter length L no greater than 1/4. Anything larger is unnecessary.
  • Begin by computing the filter in the mean-square sense, namely without using any customization or regularization and see exactly what needs to be approved upon by viewing the frequency response functions and coefficients for each explanatory series.  Good performance of the trading signal in-sample (and even out-of-sample in most cases) is meaningless unless the coefficients have solid robust characteristics in both the frequency domain and the lag domain.
  • I recommend beginning with tweaking the smoothness customization parameter expweight and the lambda_smooth regularization parameters first. Then proceed with only slight adjustments to the lambda_decay parameters. Finally, as a last resort, the lambda customization. I really never bother to look at lambda_cross. It has seldom helped in any significant manner.  Since the data we are using to target and build trading signals are log-returns, no need to ever bother with i1 and i2. Those are for the truly advanced and patient signal extractors, and should only be left for those endowed with iMetrica 😉

If you have any questions, or would like the high-frequency Yen data I used in these examples, feel free to contact me and I’ll send them to you. Until next time, happy extracting!

High-Frequency Financial Trading with Multivariate Direct Filtering I: FOREX and Futures

Posted on by
Animation 1: Click to see animation of the Japanese Yen filter in action on 164 hourly out-of-sample observations.

Animation 1: Click to see animation of the Japanese Yen filter in action on 164 hourly out-of-sample observations.

I recently acquired over 300 GBs of financial data that includes tick data for over 7000 financial assets traded on multiple markets for the past 5 years up until February 1st 2013. This USB drive packed with nearly every detail of world financial markets coupled with iMetrica gave me an opportunity to explore at any fashion to my desire the ability of multivariate direct filtering to produce high performance financial trading signals on nearly any high-frequency. Let me begin this article with saying that I am more than ecstatic with the results, as I hope you will too after reading this article.  In this first article in a series of high-frequency trading with MDFA and iMetrica that I plan to write, I provide some initial experiments with building and extracting financial trading signals for high-frequency intraday observations on foreign exchange (FOREX) data, and by high-frequency in the context of this article, I mean higher frequencies than the daily log-returns I’ve been working with in my previous articles. In the first part of this high-frequency series, I begin by exploring hourly, 30 minute, and 15 minute log-returns, and test different strategies, mostly using low-pass and the recently introduced multi-bandpass (MBP) filter to deduce the best approach to tackle the problem of building successful trading signals in higher frequency data.

In my previous articles, I was working uniquely with daily log-return data from different time spans from a year to a year and a half. This enabled the in-sample period of computing the filter coefficients for the signal extraction to include all the most recent annual phases and seasons of markets, from holiday effects, to the transitioning period of August to September that is regularly highly influential on stock market prices and commodities as trading volume increases a significant amount. One immediate question that is raised in migrating to higher-frequency intraday data is what kind of in-sample/out-of-sample time spans should be used to compute the filter in-sample and then for how long do we apply the filter out-of-sample to produce the trades? Another question that is raised with intraday data is how do we account for the close-to-open variation in price? Certainly, after close, the after-hour bids and asks will force a jump into the next trading day. How do we deal with this jump in an optimal manner? As the observation frequency gets higher, say from one hour to 30 minutes, this close-to-open jump/fall should most likely be larger. I will start by saying that, as you will see in the results of this article, with a clever choice of the extractor \Gamma and explanatory series, MDFA can handle these jumps beautifully (both aesthetically and financially). In fact, I would go so far as to say that the MDFA does a superb job in predicting the overnight variation.

One advantage of building trading signals for higher intraday frequencies is that the signals produce trading strategies that are immediately actionable. Namely one can act upon a signal to enter a long or short position immediately when they happen. In building trading signals for the daily log-return, this is not the case since the observations are not actionable points, namely the log difference of today’s ending price with yesterday’s ending price are produced after hours and thus not actionable during open market hours and only actionable the next trading day. Thus trading on intraday observations can lead to better efficiency in trading.

In this first installment in my series on high-frequency financial trading using multivariate direct filtering in iMetrica, I consider building trading signals on hourly returns of foreign exchange currencies. I’ve received a few requests after my recent articles on the Frequency Effect in seeing iMetrica and MDFA in action on the FOREX sector. So to satisfy those curiosities, I give a series of (financially) satisfying and exciting results in combining MDFA and the FOREX. I won’t give all my secretes away into building these signals (as that would of course wipe out my competitive advantage), but I will give some of the parameters and strategies used so any courageously curious reader may try them at home (or the office). In the conclusion, I give a series of even more tricks and hacks.  The results below speak for themselves  So without further ado, let the games begin.

Japanese Yen

Frequency: One hour returns
30 day out-of-sample ROI: 12 percent
Trade success ratio: 92 percent

Yen Filter Parameters: \lambda = 9.2 \alpha = 13.2, \omega_0 = \pi/5
Regularization: smooth = .918, decay = .139, decay2 = .79, cross = 0

In the first experiment, I consider hourly log-returns of a ETF index that mimics the Japanese Yen called FXY. As for one of the explanatory series, I consider the hourly log-returns of the price of GOLD which is traded on NASDAQ. The out-of-sample results of the trading signal built using a low-pass filter and the parameters above are shown in Figure 1.  The in-sample trading signal (left of cyan line) was built using 400 hourly observations of the Yen during US market hours dating back to 1 October 2012. The filter was then applied to the out-of-sample data for 180 hours, roughly 30 trading days up until Friday, 1 February 2013.

Figure 3: Out-of-sample results for the Japanese Yen. The in-sample trading signal was built using 400 hourly observations of the Yen during US market hours dating back to November 1st, 2012. The out-of-sample portion passed the cyan line is on 180 hourly observations, about 30 trading days.

Figure 1: Out-of-sample results for the Japanese Yen. The in-sample trading signal was built using 400 hourly observations of the Yen during US market hours dating back to October 1st, 2012. The out-of-sample portion passed the cyan line is on 180 hourly observations, about 30 trading days.

This beauty of this filter is that it yields a trading signal exhibiting all the characteristics that one should strive for in building a robust and successful trading filter.

  1. Consistency: The in-sample portion of the filter performs exactly as it does out-of-sample (after cyan line) in both trade success ratio and systematic trading performance. 
  2. Dropdowns: One small dropdown out-of-sample for a loss of only .8 percent (nearly the cost of the transaction).
  3. Detects the cycles as it should: Although the filter is not able to pinpoint with perfect accuracy every local small upturn during the descent of the Yen against the dollar, it does detect them nonetheless and knows when to sell at their peaks (the magenta lines).
  4. Self-correction: What I love about a robust filter is that it will tend to self-correct itself very quickly to minimize a loss in an erroneous trade. Notice how it did this in the second series of buy-sell transactions during the only loss out-of-sample. The filter detects momentum but quickly sold right before the ensuing downfall. My intuition is that only frequency-based methods such as the MDFA are able to achieve this consistently. This is the sign of a skillfully smart filter.

The coefficients for this Yen filter are shown below. Notice the smoothness of the coefficients from applying the heavy smooth regularization and the strong decay at the very end.  This is exactly the type of smooth/decay combo that one should desire. There is some obvious correlation between the first and second explanatory series in the first 30 lags or so as well. The third explanatory series seems to not provide much support until the middle lags .

Coefficients of the Yen filter. Here we use three different explanatory series to extract the trading signal shown in Figure 1.

Figure 2: Coefficients of the Yen filter. Here we use three different explanatory series to extract the trading signal.

One of the first things that I always recommend doing when first attempting to build a trading signal is to take a glance at the periodogram. Figure 2 shows the periodogram of the log-return data of the Japanese Yen over 580 hours.  Compare this with the periodogram of the same asset using log-returns of daily data over 580 days, shown in Figure 3.  Notice the much larger prominent spectral peaks at the lower frequencies in the daily log-return data. These prominent spectral peaks renders multibandpass filters much more advantageous and to use as we can take advantage of them by placing a band-pass filter directly over them to extract that particular frequency (see my article on multibandpass filters). However, in the hourly data, we don’t see any obvious spectral peaks to consider, thus I chose a low-pass filter and set the cutoff frequency at $\pi/5$, a standard choice, and good place to begin.

Figure 1: Periodogram of hourly log-returns of the Japanese Yen over 580 hours.

Figure 3: Periodogram of hourly log-returns of the Japanese Yen over 580 hours.

Figure 3: Periodogram of Japanese Yen using 580 daily log-return observations.

Figure 4: Periodogram of Japanese Yen using 580 daily log-return observations. Many more spectral peaks are present in the lower frequencies.

Japanese Yen

Frequency: 15 minute returns
7 day out-of-sample ROI: 5 percent
Trade success ratio: 82 percent

Yen Filter Parameters: \lambda = 3.7 \alpha = 13, \omega_0 = \pi/9
Regularization: smooth = .90, decay = .11, decay2 = .09, cross = 0

In the next trading experiment, I consider the Japanese Yen again, only this time I look at trading on even high-frequency log-return data than before, namely on 15 minute log-returns of the Yen from the opening bell to market close.  This presents slightly new challenges than before as the close-to-open jumps are much larger than before, but these larger jumps do not necessarily pose problems for the MDFA. In fact, I look to exploit these and take advantage to gain profit by predicting the direction of the jump.  For this higher frequency experiment, I considered 350 15-minute in-sample observations to build and optimize the trading signal, and then applied it over the span of 200 15-minute out-of-sample observations. This produced the results shown in the Figure 5 below. Out of 17 total trades out-of-sample, there were only 3 small losses each less than .5 percent drops and thus 14 gains during the 200 15-minute out-of-sample time period.  The beauty of this filter is its impeccable ability to predict the close-to-open jump in the price of the Yen. Over the nearly 7 day trading span, it was able to correctly deduce whether to buy or short-sell before market close on every single trading day change. In the figure below, the four largest close-to-open variation in Yen price is marked with a “D” and you can clearly see how well the signal was able to correctly deduce a short-sell before market close. This is also consistent with the in-sample performance as well, where you can notice the buys and/or short-sells at the largest close-to-open jumps (notice the large gain in the in-sample period right before the out-of-sample period begins, when the Yen jumped over 1 percent over night.  This performance is most likely aided by the explanatory time series I used for helping predict the close-to-open variation in the price of the Yen. In this example, I only used two explanatory series (the price of Yen, and another closely related to the Yen).

Figure : Out-of-sample performance of the Japanese Yen filter on 15 minute log-return data.

Figure 5: Out-of-sample performance of the Japanese Yen filter on 15 minute log-return data.

We look at the filter transfer functions to see what frequencies they are being privileged in the construction of the filter. Notice that some noise leaks out passed the frequency cutoff at \pi/9, but this is typically normal and a non-issue. I had to balance for both timeliness and smoothness in this filter using both the customization parameters \lambda and \alpha. Not much at frequency 0 is emphasized, with more emphasis stemming from the large spectral peak found right at \pi/9.

Figure : The filter transfer functions.

Figure 6: The filter transfer functions.

British Pound

Frequency: 30 minute returns
14 day out-of-sample ROI: 4 percent
Trade success ratio: 76 percent

British Pound Filter Parameters: \lambda = 5 \alpha = 15, \omega_0 = \pi/9
Regularization: smooth = .109, decay = .165, decay2 = .19, cross = 0

In this example we consider the frequency of the data to 30 minute returns and attempt to build a robust trading signal for a derivative of the British Pound (BP) on this higher frequency. Instead of using the cash value of the BP, I use 30 minute returns of the BP Futures contract expiring in March (BPH3). Although I don’t have access to tick data from the FOREX, I do have tick data from GLOBEX for the past 5 years.  Thus the futures series won’t be an exact replication of the cash price series of the BP, but it should be quite close due to very low interest rates.

The results of the out-of-sample performance of the BP futures filter are shown in Figure 7. I constructed the filter using an initial in-sample size of 390 30 minute returns dating back to 1 December 2012. After pinpointing a frequency cutoff in the frequency domain for the \Gamma that yielded decent trading results in-sample, I then proceeded to optimize the filter in-sample on smoothness and regularization to achieve similar out-of-sample performance. Applying the resulting filter out-of-sample on 168 30-minute log-return observations of the BP futures series along with 3 explanatory series, I get the results shown below. There were 13 trades made and 10 of them were successful. Notice that the filter does an exquisite job at triggering trades near local optimums associated with the frequencies inside the cutoff of the filter.

Figure 5: The out-of-sample results of the British Pound using 30-minute return data.

Figure 7: The out-of-sample results of the British Pound using 30-minute return data.

In looking at the coefficients of the filter for each series in the extraction, we can clearly see the effects of the regularization: the smoothness of the coefficients the fast decay at the very end. Notice that I never really apply any cross regularization to stress the latitudinal likeliness between the 3 explanatory series as I feel this would detract from the predicting advantages brought by the explanatory series that I used.

Figure 6: The coefficients for the 3 explanatory series of the BP futures,

Figure 8: The coefficients for the 3 explanatory series of the BP futures,

Euro

Frequency: 30 min returns
30 day out-of-sample ROI: 4 percent
Trade success ratio: 71 percent

Euro Filter Parameters: \lambda = 0, \alpha = 6.4, \omega_0 = \pi/9
Regularization: smooth = .85, decay = .27, decay2 = .12, cross = .001

Continuing with the 30 minute frequency of log-returns, in this example I build a trading signal for the Euro futures contract with expiration on 18 March 2013 (UROH3 on the GLOBEX). My in-sample period, being the same as my previous experiment, is from 1 December 2012 to 4 January 2013 on 30 minute returns using three explanatory time series.  In this example, after inspecting the periodogram, I decided upon a low-pass filter with a frequency cutoff of \pi/9. After optimizing the customization and applying the filter to one month of 30 minute frequency return data out-of-sample (month of January 2013, after cyan line) we see the performance is akin to the performance in-sample, exactly what one strives for. This is due primarily to the heavy regularization of the filter coefficients involved. Only four very small losses of less than .02 percent are suffered during the out-of-sample span that includes 10 successful trades, with the losses only due to the transaction costs. Without transaction costs, there is only one loss suffered at the very beginning of the out-of-sample period.

Figure : Out-of-sample performance on the 30-min log-returns of Euro futures contract UROH3.

Figure 9 : Out-of-sample performance on the 30-min log-returns of Euro futures contract UROH3.

As in the first example using hourly returns, this filter again exhibits the desired characteristics of a robust and high-performing financial trading filter. Notice the out-of-sample performance behaves akin to the in-sample performance, where large upswings and downswings are pinpointed to high-accuracy. In fact, this is where the filter performs best during these periods. No need for taking advantage of a multibandpass filter here, all the profitable trading frequencies are found at less than \pi/9.  Just as with the previous two experiments with the Yen and the British Pound, notice that the filter cleanly predicts the close-to-open variation (jump or drop) in the futures value and buys or sells as needed.  This can be seen from many of the large jumps in the out-of-sample period (after cyan line).

One reason why these trading signals perform so well is due to their approximation power of the symmetric filter. In comparing the trading signal (green) with a high-order approximation of the symmetric filter (gray line) transfer function \Gamma shown in Figure 10, we see that trading signal does an outstanding job at approximating the symmetric filter uniformly. Even at the latest observation (the right most point), the asymmetric filter hones in on the symmetric signal (gray line) with near perfection. Most importantly, the signal crosses zero almost exactly where required.  This is exactly what you want when building a high-performing trading signal.

Figure : Plot of approximation of the real-time trading signal for UROH3 with a high order approximation of the symmetric filter transfer function.

Figure 10: Plot of approximation of the real-time trading signal for UROH3 with a high order approximation of the symmetric filter transfer function.

In looking at the periodogram of the log-return data and the output trading signal differences (colored in blue), we see that the majority of the frequencies were accounted for as expected in comparing the signal with the symmetric signal. Only an inconsequential amount of noise leakage passed the frequency cutoff of \pi/9 is found.  Notice the larger trading frequencies, the more prominent spectral peaks, are located just after \pi/6. These could be taken into account with a smart multibandpass filter in order to manifest even more trades, but I wanted to keep things simple for my first trials with high-frequency foreign exchange data.  I’m quite content with the results that I’ve achieved so far.

Figure : Comparing the periodogram of the signal with the log-return data.

Figure 11: Comparing the periodogram of the signal with the log-return data.

Conclusion

I must admit, at first I was a bit skeptical of the effectiveness that the MDFA would have in building any sort of successful trading signal for FOREX/GLOBEX high frequency data. I always considered the FOREX market rather ‘efficient’ due to the fact that it receives one of the highest trading volumes in the world.  Most strategies that supposedly work well on high-frequency FOREX all seem to use some form of technical analysis or charting (techniques I’m particularly not very fond of), most of which are purely time-domain based. The direct filter approach is a completely different beast, utilizing a transformation into the frequency domain and a ‘bending and warping’ of the metric space for the filter coefficients to extract a signal within the noise that is the log-return data of financial assets.  For the MDFA to be very effective at building timely trading signals, the log-returns of the asset need to diverge from white noise a bit, giving room for pinpointing intrinsically important cycles in the data. However, after weeks of experimenting, I have discovered that building financial trading signals using MDFA and iMetrica on FOREX data is as rewarding as any other.

As my confidence has now been bolstered and amplified even more after my experience with building financial trading signals with MDFA and iMetrica for high-frequency data on foreign exchange log-returns at nearly any frequency, I’d be willing to engage in a friendly competition with anyone out there who is certain that they can build better trading strategies using time domain based methods such as technical analysis or any other statistical arbitrage technique.  I strongly believe these frequency based methods are the way to go, and the new wave in financial trading.  But it takes experience and a good eye for the frequency domain and periodograms to get used to. I haven’t seen many trading benchmarks that utilize other types of strategies, but i’m willing to bet that they are not as consistent as these results using this large of an out-of-sample to in-sample ratio (the ratios in these experiments were between .50 and .80).  If anyone would like to take me up on my offer for a friendly competition (or know anyone that would), feel free to contact me.

After working with a multitude of different financial time series and building many different types of filters, I have come to the point where I can almost eyeball many of the filter parameter choices including the most important ones being the extractor \Gamma along with the regularization parameters, without resorting to time consuming, and many times inconsistent, optimization routines.  Thanks to iMetrica, transitioning from visualizing the periodogram to the transfer functions and to the filter coefficients and back to the time domain to compare with the approximate symmetric filter in order to gauge parameter choices is an easy task, and an imperative one if one wants to build successful trading signals using MDFA.

Here are some overall tips and tricks to build your own high performance trading signals on high-frequency data at home:

  • Pay close attention to the periodogram. This is your best friend in choosing the extractor \Gamma. The best performing signals are not the ones that trade often, but trade on the most important frequencies found in the data. Not all frequencies are created equal. This is true when building either low-pass or multibandpass frequencies. 
  • When tweaking customization, always begin with \alpha, the parameter for smoothness. \lambda for timeliness should be the last resort. In fact, this parameter will most likely be next to useless due to the fact that the log-return of financial data is stationary. You probably won’t ever need it.
  • You don’t need many explanatory series. Like most things in life, quality is superior to quantity. Using the log-return data of the asset you’re trading along with one and maybe two explanatory series that somewhat correlate with the financial asset you’re trading on is sufficient. Anymore than that is ridiculous overkill, probably leading to over-fitting (even the power of regularization at your fingertips won’t help you).

In my next article, I will continue with even more high-frequency trading strategies with the MDFA and iMetrica where I will engage in the sector of Funds and ETFs. If any curious reader would like even more advice/hints/comments on how to build these trading signals on high-frequency data for the FOREX (or the coefficients built in these examples), feel free to get in contact with me via email. I’ll be happy to help.

Happy extracting!