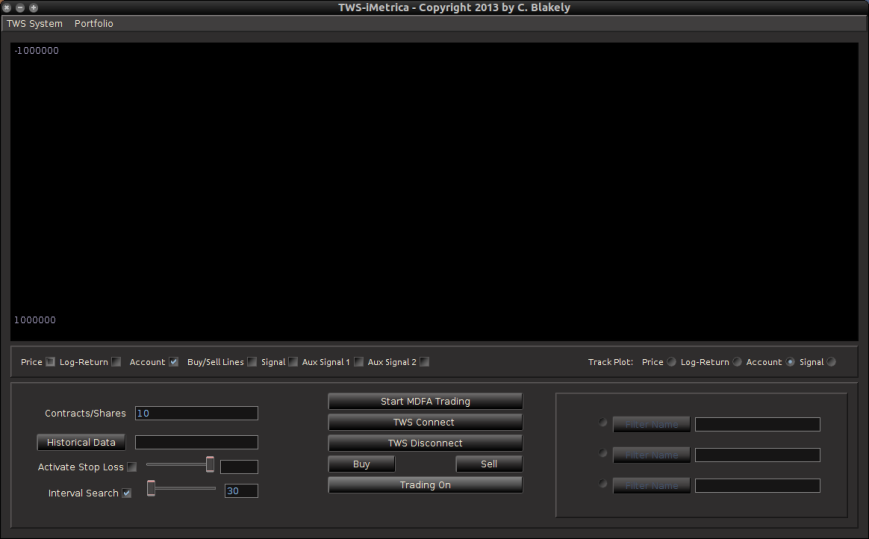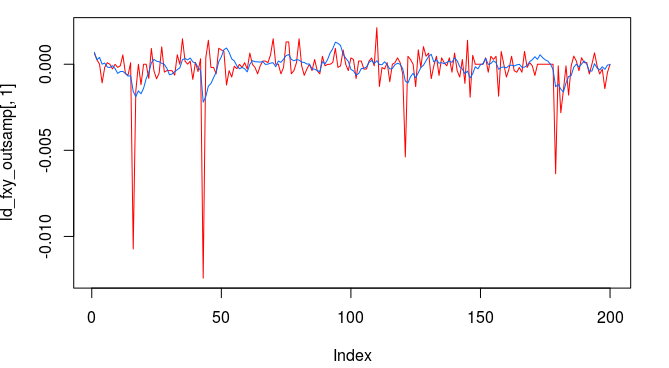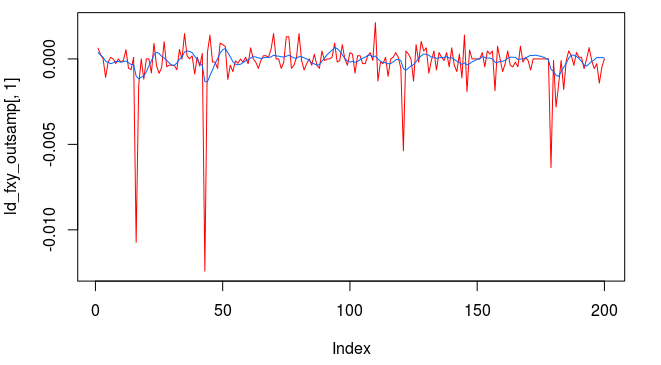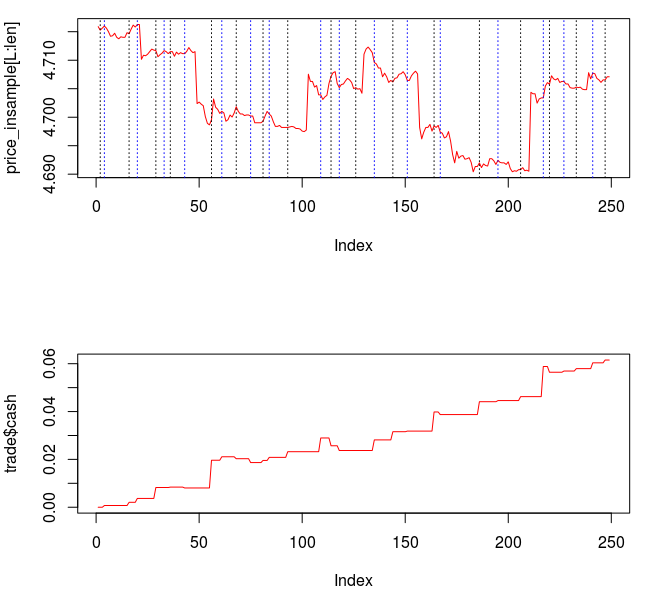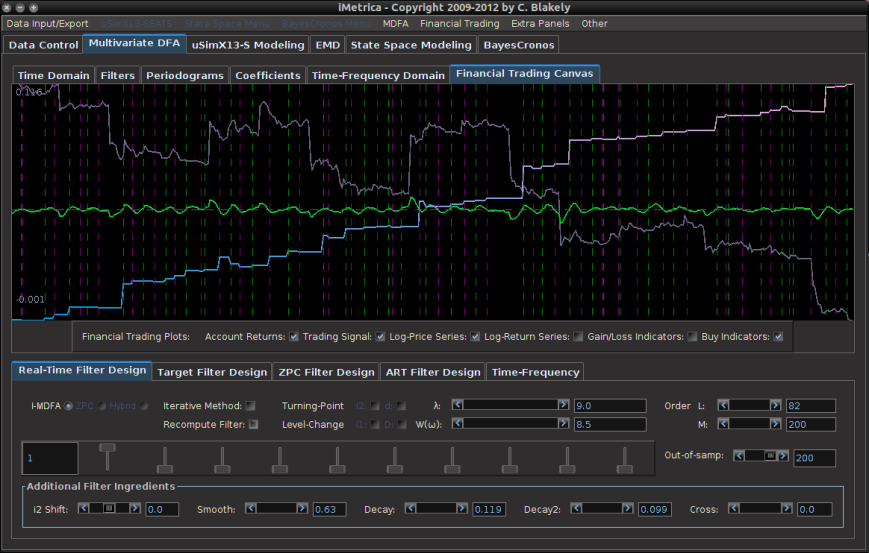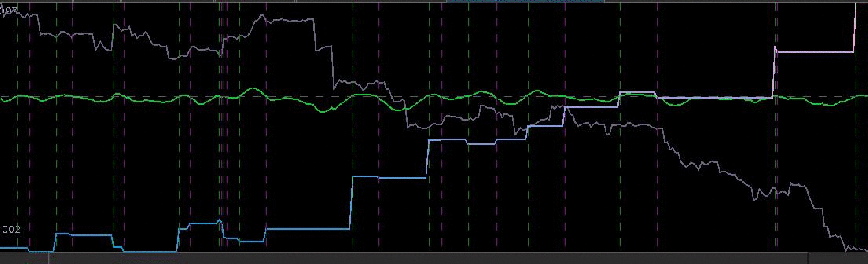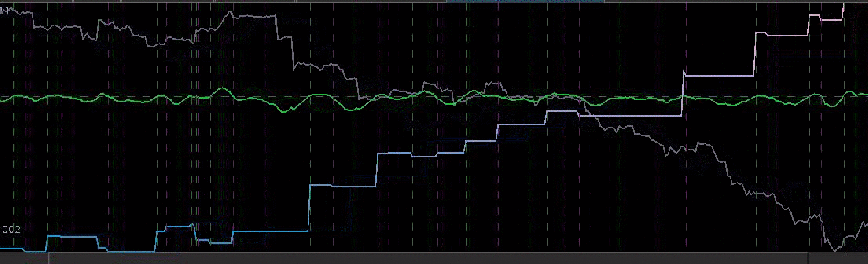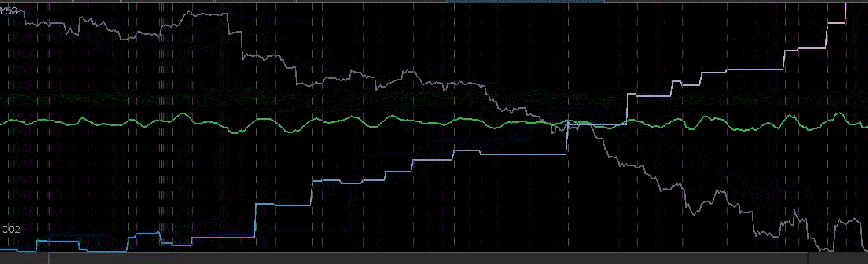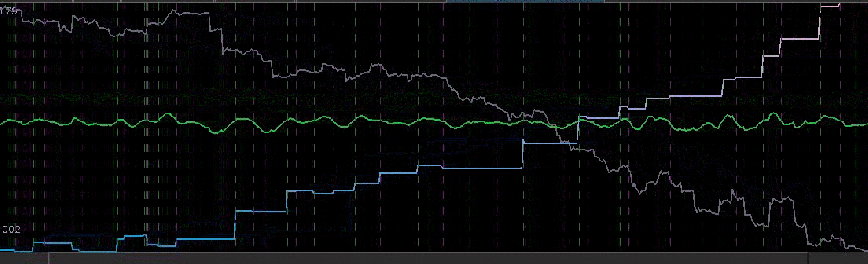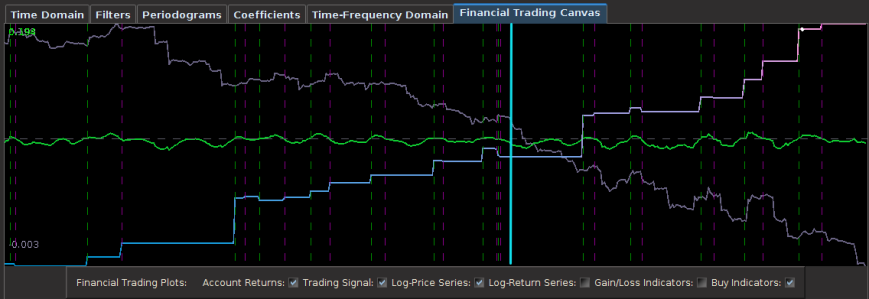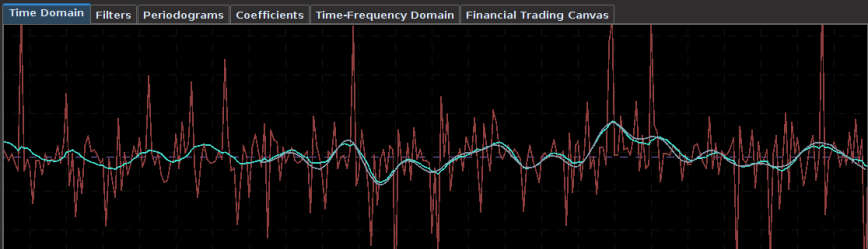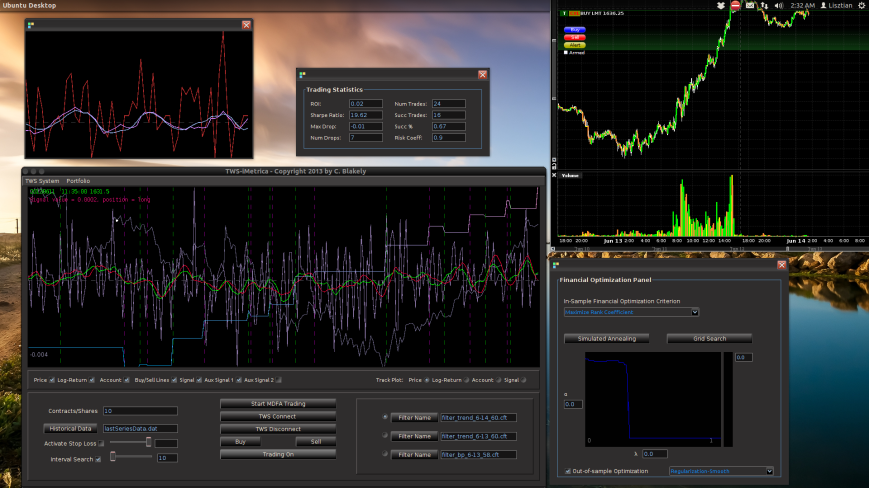
Figure 1: The TWS-iMetrica automated financial trading platform. Featuring fast performance optimization, analysis, and trading design features unique to iMetrica for building direct real-time filters to generate automated trading signals for nearly any tradeable financial asset. The system was built using Java, C, and the Interactive Brokers IB API in Java.
Introduction
I realize that I’ve been MIA (missing in action for non-anglophones) the past three months on this blog, but I assure you there has been good reason for my long absence. Not only have I developed a large slew of various optimization, analysis, and statistical tools in iMetrica for constructing high-performance financial trading signals geared towards intraday trading which I will (slowly) be sharing over the next several months (with some of the secret-sauce-recipes kept to myself and my current clients of course), but I have also built, engineered, tested, and finally put into commission on a daily basis the planet’s first automated financial trading platform completely based on the recently developed FT-AMDFA (adaptive multivariate direct filtering approach for financial trading). I introduce to you iMetrica’s little sister, TWS-iMetrica.
Coupled with the original software I developed for hybrid econometrics, time series analysis, signal extraction, and multivariate direct filter engineering called iMetrica, the TWS-iMetrica platform was built in a way to provide an easy to use yet powerful, adaptive, versatile, and automated trading machine for intraday financial trading with a variety of options for building your own day trading strategies using MDFA based on your own financial priorities. Being written completely in Java and gnu c, the TWS-iMetrica system currently uses the Interactive Brokers (IB) trading workstation (TWS) Java API in order to construct the automated trades, connect to the necessary historical data feeds, and provide a variety of tick data. Thus in order to run, the system will require an activated IB trading account. However, as I discuss in the conclusion of this article, the software was written in a way to be seamlessly adapted to any other brokerage/trading platform API, as long as the API is available in Java or has Java wrappers available.
The steps for setting up and building an intraday financial trading environment using iMetrica + TWS-iMetrica are easy. There are four of them. No technical analysis indicator garbage is used here, no time domain methodologies, or stochastic calculus. TWS-iMetrica is based completely on the frequency domain approach to building robust real-time multivariate filters that are designed to extract signals from tradable financial assets at any fixed observation of frequencies (the most commonly used in my trading experience with FT-AMDFA being 5, 15, 30, or 60 minute intervals). What makes this paradigm of financial trading versatile is the ability to construct trading signals based on your own trading priorities with each filter designed uniquely for a targeted asset to be traded. With that being said, the four main steps using both iMetrica and TWS-iMetrica are as follows:
- The first step to building an intraday trading environment is to construct what I call an MDFA portfolio (which I’ll define in a brief moment). This is achieved in the TWS-iMetrica interface that is endowed with a user-friendly portfolio construction panel shown below in Figure 4.
- With the desired MDFA portfolio, selected, one then proceeds in connecting TWS-iMetrica to IB by simply pressing the Connect button on the interface in order to download the historical data (see Figure 3).
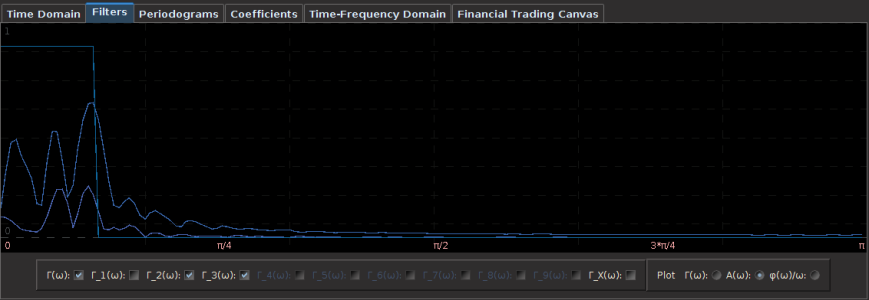
- With the historical data saved, the iMetrica software is then used to upload the saved historical data and build the filters for the given portfolio using the MDFA module in iMetrica (see Figure 2). The filters are constructed using a sequence of proprietary MDFA optimization and analysis tools. Within the iMetrica MDFA module, three different types of filters can be built 1) a trend filter that extracts a fast moving trend 2) a band-pass filter for extracting local cycles, and 3) A multi-bandpass filter that extracts both a slow moving trend and local cycles simultaneously.
- Once the filters are constructed and saved in a file (a .cft file), the TWS-iMetrica system is ready to be used for intrady trading using the newly constructed and optimized filters (see Figure 6).
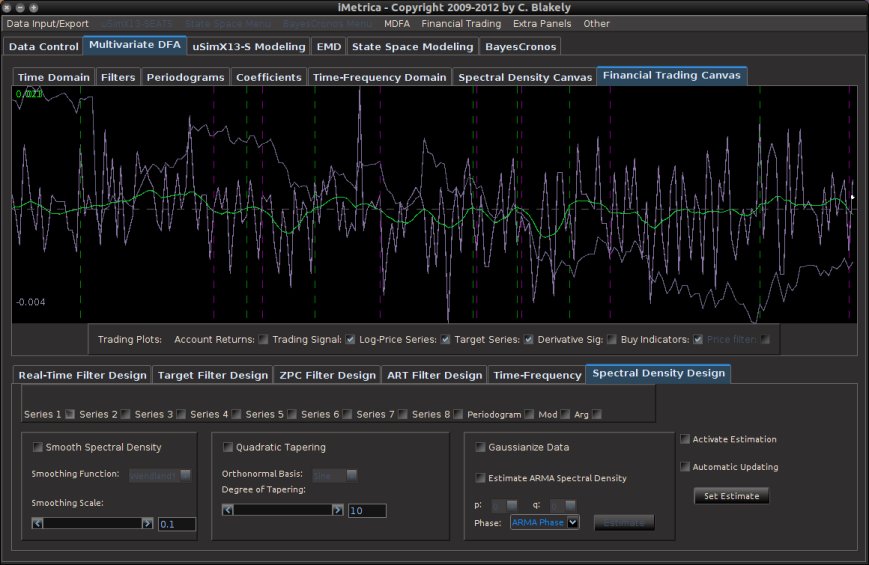
Figure 2: The iMetrica MDFA module for constructing the trading filters. Features dozens of design, analysis, and optimization components to fit the trading priorities of the user and is used in conjunction with the TWS-iMetrica interface.
In the remaining part of this article, I give an overview of the main features of the TWS-iMetrica software and how easily one can create a high-performing automated trading strategy that fits the needs of the user.
The TWS-iMetrica Interface
The main TWS-iMetrica graphical user interface is composed of several components that allow for constructing a multitude of various MDFA intraday trading strategies, depending on one’s trading priorities. Figure 3 shows the layout of the GUI after first being launched. The first component is the top menu featuring TWS System, some basic TWS connection variables which, in most cases, these variables are left in their default mode, and the Portfolio menu. To access the main menu for setting up the MDFA trading environment, click Setup MDFA Portfolio under the Portfolio menu. Once this is clicked, a panel is displayed (shown in Figure 4) featuring the required a priori parameters for building the MDFA trading environment that should all be filled before MDFA filter construction and trading is to take place. The parameters and their possible values are given below Figure 4.
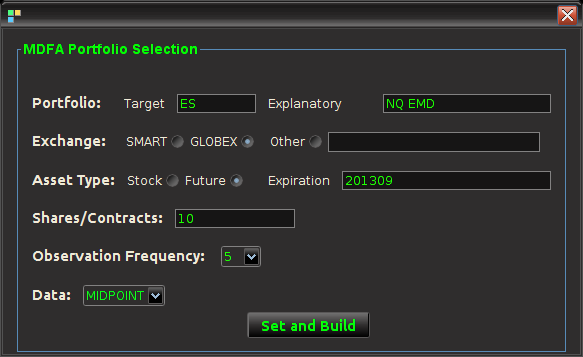
Figure 4 – The Setup MDFA Portfolio panel featuring all the setting necessary to construct the automated trading MDFA environment.
- Portfolio – The portfolio is the basis for the MDFA trading platform and consists of two types of assets 1) The target asset from which we construct the trading signal, engineer the trades, and use in building the MDFA filter 2) The explanatory assets that provide the explanatory data for the target asset in the multivariate filter construction. Here, one can select up to four explanatory assets.
- Exchange – The exchange on which the assets are traded (according to IB).
- Asset Type – If the input portfolio is a selection of Stocks or Futures (Currencies and Options soon to be available).
- Expiration – If trading Futures, the expiration date of the contract, given as a six digit number of year then month (e.g. 201306 for June 2013).
- Shares/Contracts – The number of shares/contracts to trade (this number can also be changed throughout the trading day through the main panel).
- Observation frequency – In the MDFA financial trading method, we consider uniformly sampled observations of market data on which to do the trading (in seconds). The options are 1, 2, 3, 5, 15, 30, and 60 minute data. The default is 5 minutes.
- Data – For the intraday observations, determines the nature of data being extracted. Valid values include TRADES, MIDPOINT, BID, ASK, and BID_ASK. The default is MIDPOINT
- Historical Data – Selects how many days are used to for downloading the historical data to compute the initial MDFA filters. The historical data will of course come in intervals chosen in the observation frequency.
Once all the values have been set for the MDFA portfolio, click the Set and Build button which will first begin to check if the values entered are valid and if so, create the necessary data sets for TWS-iMetrica to initialize trading. This all must be done while TWS-iMetrica is connected to IB (not set in trading mode however). If the build was successful, the historical data of the desired target financial asset up to the most recent observation in regular market trading hours will be plotted on the graphics canvas. The historical data will be saved to a file named (by default) “lastSeriesData.dat” and the data will be come in columns, where the first column is the date/time of the observation, the second column is the price of the target asset, and remaining columns are log-returns of the target and explanatory data. And that’s it, the system is now setup to be used for financial trading. These values entered in the Setup MDFA Portfolio will never have to be set again (unless changes to the MDFA portfolio are needed of course).
Continuing on to the other controls and features of TWS-iMetrica, once the portfolio has been set, one can proceed to change any of the settings in main trading control panel. All these controls can be used/modified intraday while in automated MDFA trading mode. In the left most side of the panel at the main control panel (Figure 5) of the interface includes a set of options for the following features:
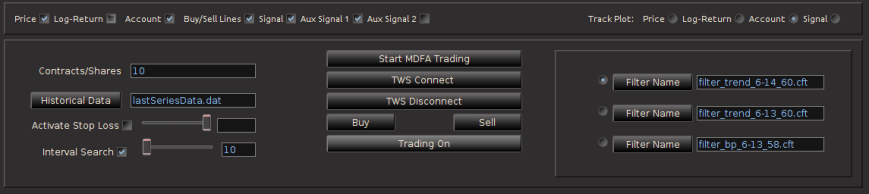
Figure 5 – The main control panel for choosing and/or modifying all the options during intraday trading.
- In contracts/shares text field, one enters the amount of share (for stocks) or contracts (for futures) that one will trade throughout the day. This can be adjusted during the day while the automated trading is activated, however, one must be certain that at the end of the day, the balance between bought and shorted contracts is zero, otherwise, you risk keeping contracts or shares overnight into the next trading day.Typically, this is set at the beginning before automated trading takes place and left alone.
- The data input file for loading historical data. The name of this file determines where the historical data associated with the MDFA portfolio constructed will be stored. This historical data will be needed in order to build the MDFA filters. By default this is “lastSeriesData.dat”. Usually this doesn’t need to be modified.
- The stop-loss activation and stop-loss slider bar, one can turn on/off the stop-loss and the stop-loss amount. This value determines how/where a stop-loss will be triggered relative to the price being bought/sold at and is completely dependent on the asset being traded.
- The interval search that determines how and when the trades will be made when the selected MDFA signal triggers a buy/sell transaction. If turned off, the transaction (a limit order determined by the bid/ask) will be made at the exact time that the buy/sell signal is triggered by the filter. If turned on, the value in the text field next to it gives how often (in seconds) the trade looks for a better price to make the transaction. This search runs until the next observation for the MDFA filter. For example, if 5 minute return data is being used to do the trading, the search looks every n seconds for 5 minutes for a better price to make the given transaction. If at the end of the 5 minute period no better price has been found, the transaction is is made at the current ask/bid price. This feature has been shown to be quite useful during sideways or highly volatile markets.
The middle of the main control panel features the main buttons for both connecting to disconnecting from Interactive Brokers, initiating the MDFA automated trading environment, as well as convenient buttons used for instantaneous buy/sell triggers that supplement the automated system. It also features an on/off toggle button for activating the trades given in the MDFA automated trading environment. When checked on, transactions according to the automated MDFA environment will proceed and go through to the IB account. If turned off, the real-time market data feeds and historical data will continue to be read into the TWS-iMetrica system and the signals according to the filters will be automatically computed, but no actual transactions/trades into the IB account will be made.
Finally, on the right hand side of the main control panel features the filter uploading and selection boxes. These are the MDFA filters that are constructed using the MDFA module in iMetrica. One convenient and useful feature of TWS-iMetrica is the ability to utilize up to three direct real-time filters in parallel and to switch at any given moment during market hours between the filters. (Such a feature enhances the adaptability of the trading using MDFA filters. I’ll discuss more about this in further detail shortly). In order to select up to three filters simultaneously, there is a filter selection panel (shown in bottom right corner of Figure 6 below) displaying three separate file choosers and a radio button corresponding to each filter. Clicking on the filter load button produces a file dialog box from which one selects a filter (a *.cft file produced by iMetrica). Once the filter is loaded properly, on success, the name of the filter is displayed in the text box to the right, and the radio button to the left is enabled. With multiple filters loaded, to select between any of them, simply click on their respective radio button and the corresponding signal will be plotted on the plot canvas (assuming market data has been loaded into the TWS-iMetrica using the market data file upload and/or has been connected to the IB TWS for live market data feeds). This is shown in Figure 6.

Figure 6 – The TWS-iMetrica main trading interface features many control options to design your own automated MDFA trading strategies.
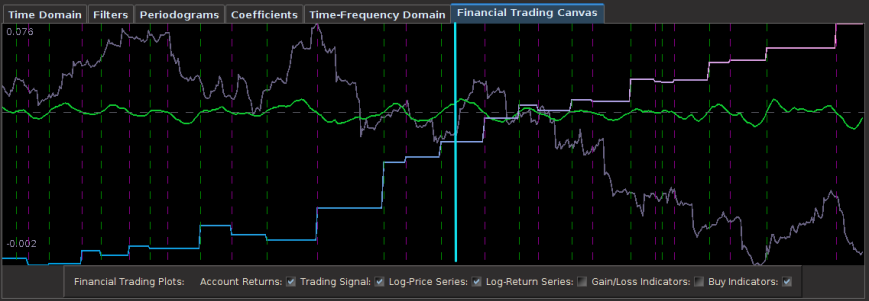
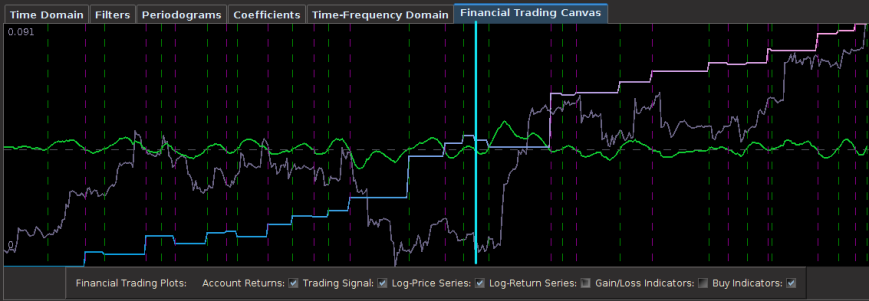
And finally, once the historical data file for the MDFA portfolio has been created, up to three filters have been created for the portfolio and entered in the filter selection boxes, and the system is connected to Interactive Brokers by pressing the Connect button, the market and signal plot panel can then be used for visualizing the different components that one will need for analyzing the market, signal, and performance of the automated trading environment. In the panel just below the plot canvas features and array of checkboxes and radiobuttons. When connected to IB and the Start MDFA Trading has been pressed, all the data and plots are updated in real-time automatically at the specific observation frequency selected in the MDFA Portfolio setup. The currently available plots are as follows:
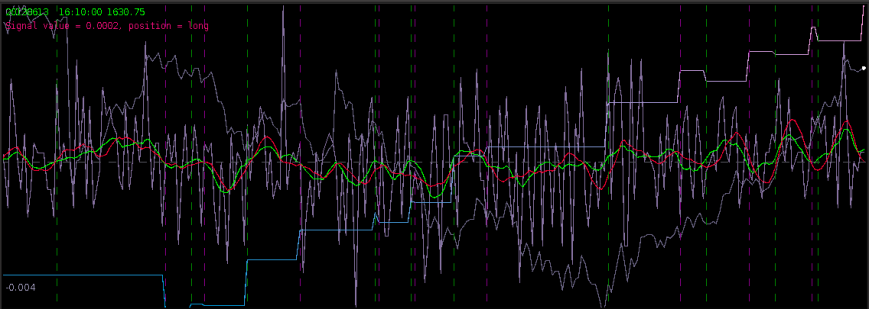
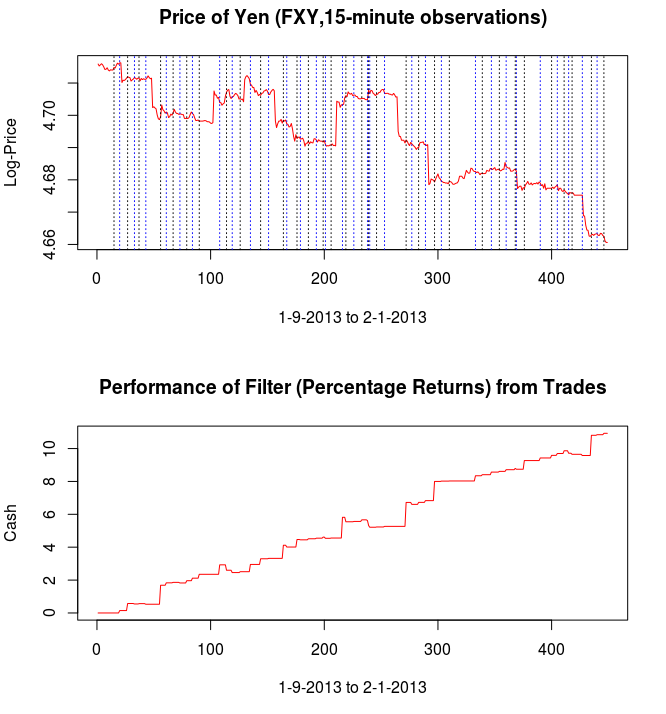
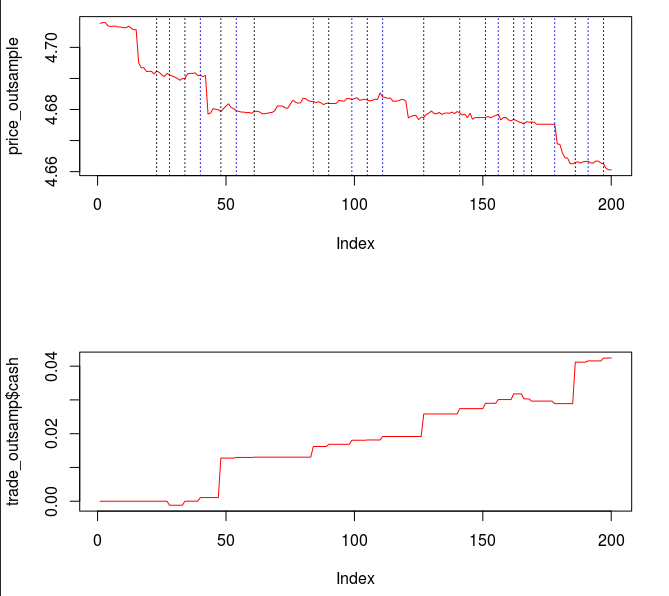
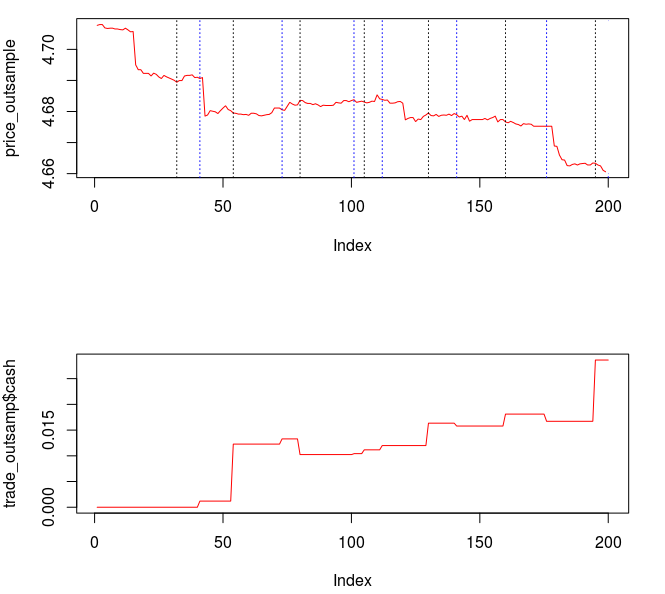
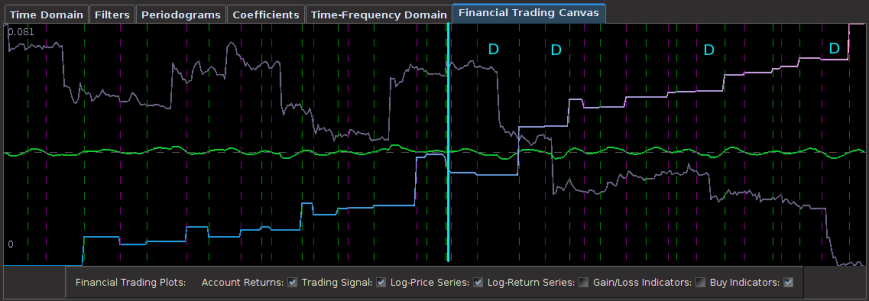
Figure 8 – The plots for the trading interface. Features price, log-return, account cumulative returns, signal, buy/sell lines, and up to two additional auxiliary signals.
- Price – Plots in real-time the price of the asset being traded, at the specific observation frequency selected for the MDFA portfolio.
- Log-returns – Plots in real-time the log-returns of the price, which is the data that is being filtered to construct the trading signal.
- Account – Shows the cumulative returns produced by the currently chosen MDFA filter over the current and historical data period (note that this does not necessary reflect the actual returns made by the strategy in IB, just the theoretical returns over time if this particular filter had been used).
- Buy/Sell lines – Shows dashed lines where the MDFA trading signal has produced a buy/sell transaction. The green lines are the buy signals (entered a long position) and magenta lines are the sell (entered a short position).
- Signal – The plot of the signal in real-time. When new data becomes available, the signal is automatically computed and replotted in real-time. This gives one the ability to closely monitory how the current filter is reacting to the incoming data.
- Aux Signal 1/2 – (If available) Plots of the other available signals produced by the (up to two) other filters constructed and entered in the system. To make either of these auxillary signals the main trading signal simply select the filter associated with the signal using the radio buttons in the filter selection panel.
Along with these plots, to track specific values of any of these plots at anytime, select the desired plot in the Track Plot region of the panel bar. Once selected, specific values and their respective times/dates are displayed in the upper left corner of the plot panel by simply placing the mouse cursor over the plot panel. A small tracking ball will then be moved along the specific plot in accordance with movements by the mouse cursor.
With the graphics panel displaying the performance in real-time of each filter, one can seamlessly switch between a band-pass filter or a timely trend (low-pass) filter according to the changing intraday market conditions. To give an example, suppose at early morning trading hours there is an unusual high amount of volume pushing an uptrend or pulling a downtrend. In such conditions a trend filter is much more appropriate, being able to follow the large-variation in log-returns much better than a band-pass filter can. One can glean from the effects of the trend filter on the morning hours of the market. After automated trading using the trend filter, with the volume diffusing into the noon hour, the band-pass filter can then be applied in order to extract and trade at certain low frequency cycles in the log-return data. Towards the end of the day, with volume continuously picking up, the trend filter can then be selected again in order to track and trade any trending movement automatically.
I am in the process of currently building an automated algorithm to “intelligently” switch between the uploaded filters according to the instantaneous market conditions (with triggering of the switching being set by volume and volatility. Otherwise, for the time being, currently the user must manually switch between different filters, if such switching is at all desired (in most cases, I prefer to leave one filter running all day. Since the process is automated, I prefer to have minimal (if any) interaction with the software during the day while it’s in automated trading mode).
Conclusion
As I mentioned earlier, the main components of the TWS-iMetrica were written in a way to be adaptable to other brokerage/trading APIs. The only major condition is that the API either be available in Java, or at least have (possibly third-party?) wrappers available in Java. That being said, there are only three main types of general calls that are made automated to the connected broker 1) retrieve historical data for any asset(s), at any given time, at most commonly used observation frequencies (e.g. 1 min, 5 min, 10 min, etc.), 2) subscribe to automatic feed of bar/tick data to retrieve latest OHLC and bid/ask data, and finally 3) Place an order (buy/sell) to the broker with different any order conditions (limit, stop-loss, market order, etc.) for any given asset.
If you are interested in having TWS-iMetrica be built for your particular brokerage/trading platform (other than IB of course) and the above conditions for the API are met, I am more than happy to be hired at certain fixed compensation, simply get in contact with me. If you are interested seeing how well the automated system has performed thus far, interested in future collaboration, or becoming a client in order to use the TWS-iMetrica platform, feel free to contact me as well.
Happy extracting!